Explanation

This question involves a region in the xy plane. Since the inequality is less than or equal to, the region will be defined by everything that is left and below the line 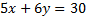. That line can be put into 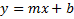form by subtracting 5x from both sides of the equation and dividing by 6, giving us



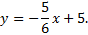
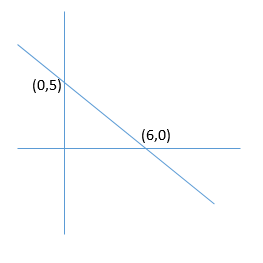
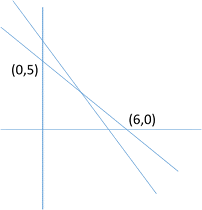
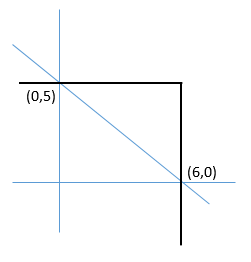
On this line, when x=0, y=5; 5 is the y-intercept. The line slopes down to the right at a moderate angle and crosses the x-axis when y is zero, so that 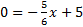and 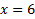. Indeed, while the line format 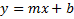is generally useful, the format 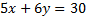allows us to see the x- and y-intercepts easily. We would go ahead and sketch the line on our noteboard:



On to the data statements, evaluating them first separately.

Statement (1) describes a similar but different line to the border of Region R. It can quickly be judged insufficient on the grounds that it is a line with a different slope than the boundary line of region R. You might react, "Wait a minute. The question said (r, s) was a point--why are we talking about a line of r and s, then?" We are talking about a line because Statement (1) has not uniquely defined r and s for us. (r, s) is, indeed, a point, but on the basis of 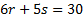, we can only narrow down the field of possibilities. 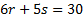A line is a collection of points, and the line describes all the possible locations of (r, s). If this line lies either wholly inside or wholly outside region R, then we will be able to answer the question of whether (r, s) is inside the region for all possible cases. On the other hand, if the line of possible locations for (r, s) is partly inside and partly outside region R, then we will not be able to answer the question definitively, because in some possible cases (r, s) is inside region R and in other possible cases it's outside region R. This latter possibility is, in fact, the reality. The line 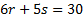has y-intercept of 6 and an x-intercept of 5; the values are switched from the intercepts of the border of region R. As you can sketch or imagine, the two lines cross like an elongated diagonal letter X.



Indeed, the only way a line would not cross the border of region R would be for that line to be parallel to that border, since any pair of non-parallel lines will cross eventually. By this alternate train of thought, you could compute the slope of this line as 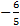, using the intercepts and the fact that slope is . Statement (1) is insufficient.

Statement (2) describes the range of possibilities for the point (r, s) with two boundaries. Since each boundary is parallel to an axis, Statement (2) describes a box-like corner boundary that includes everything to the left and down similar to region R.



The upper-right triangle is permitted by Statement (2), as it's inside the box, but it's outside of region R. Meanwhile, the region described by Statement (2) also includes plenty of points within region R. Once again, based on the data in this statement, the point could be either inside or outside of region R, so we are unable to answer the question definitively. Statement (2) is insufficient.

We must combine the statements. When both Statements are true, the field of possibilities is significantly reduced. The point must now be on the line 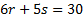and within the rectangular boundary:



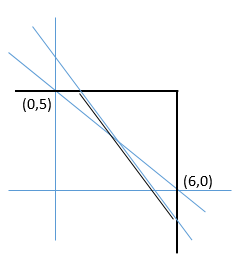
The remaining line segment still has a portion inside of region R and outside of region R. So the statements together are insufficient. We can double-check and make sure we haven't drawn incorrectly by cases. The point (5,0) is on the line 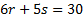and it satisfies the condition 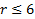. That point is inside region R. It's a little trickier to come up with a point that is in the short segment above region R. Since , we can choose a value of s that is near 5 but less: say, 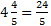. Then 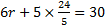, , 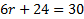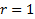. So 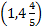is on the line segment. 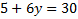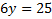If we plug r=1 into the boundary line, we get , so and 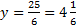. Since 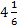is less than 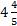, the possible (r,s) value we are looking at is on the line described in Statement (1), inside the boundary described by Statement (2), and outside (above) the region R.

The correct answer is (E).