Explanation

One way, but not the only way, for these triangles to have the same area would be for them to have the same side lengths and angles. We can already tell that's not the case here, because ST and PQ are equal length but across from angles of different measures, since one is across from a right angle and one is across from a non-right angle. We'll need to find out a valid base-height pair for each triangle, or an accurate comparison of how valid base-height pairs compare without knowing the exact values. Let's turn to the data statements, separately first.

Statement (1) looks pretty useful because it compares two heights of possible valid base-height pairs in these triangles. Now triangle PQR has a base of x and a height of PR, so it's area is 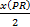. The area of PST is its height, which we can call 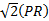, times half its base, which we don't know but can attempt to get from the Pythagorean Theorem:







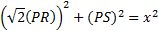
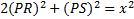
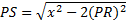
That ugly thing is the base of PST, so its base times height, halved, is:



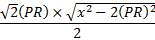
Is this definitively the same as the area of the other triangle? It is if and only if













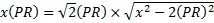
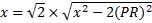
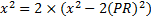
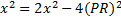
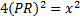
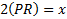
This might seem likely, but we don't know it. Insufficient.

Statement (2) tells us that triangle PST is isosceles, meaning that PT = PS. That also means that triangle PST is a 45-45-90 triangle, and hence the lengths of the sides are in the ratio 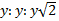(we should use a different variable, y's and not x's, because we already have an x present here). This will allow us to determine the area of triangle PST in terms of x. However, we can't quite determine the area of PQR in terms of x, because we know nothing about the length PR or RQ or the angle measures. This statement gives us some information, but not enough to be able to compare the areas of the triangles definitively. Hence Statement (2) is insufficient.

Combining the statements, we can see conceptually that we have sufficient information. Statement (1) wasn't sufficient because we didn't know whether 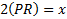. But Statement (2) allows us to solve for PT in terms of x, and Statement (1) gives a direct comparison between PT and PR, so together we will fill in the piece missing from Statement (1).

Alternate logic to use to combine the statements is to start with what's missing not from Statement (1), but from Statement (2). When we had Statement (2) alone, we had solved for the sides PST in terms of x, but we didn't know the height of PR. Statement (1) gives us this height in terms of one of the sides of the other triangle. So, either way, the statements together are sufficient.

The correct answer is (C).