Solving Two Linear Equations
Solving by Substitution
To solve a system of linear equations without graphing, you can use the substitution method. This method works by solving one of the linear equations for one of the variables, then substituting this value for the same variable in the other linear equation and solving for the other variable. It does not matter which equation you choose first, or which variable you solve for first.
Let’s use substitution to solve this system of two linear equations:
![]()
![]()
First, choose one of the equations and solve it for either x or y. We can start with the second equation and solve for y, since it doesn’t have a coefficient:
![]()
![]()
Now we have a value, 24 – 4x, for y. We substitute this value of y into the first equation to obtain:
![]()
We now have one equation and one variable. We can solve for x.
![]()
![]()
![]()
![]()
![]()
If x happened to be all we needed, we’re done. But if we also need y, we’ll plug the value of x back into either original equation. Say we choose the second equation:
![]()
![]()
![]()
![]()
The solution to this system of linear equations is x = 5, y = 4. This can also be written as (x, y) = (5, 4).
Solving by Combination
The basic principle of solving by combination is to manipulate two equations so that, when the equations are added together, one of the variables cancels out. Since one of the variables cancels, this method is sometimes called the elimination method.
Let’s use combination to solve this system of two equations:
![]()
![]()
This system of equations is suited for combination, because there is already a 2x in both equations. Therefore, if we subtract equation (1) from equation (2) – or, equivalently, multiply equation (1) by -1 and add the two equations – we have a single equation with y:
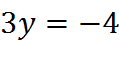
Dividing both sides, we find that y = -4/3. We can then plug y back into either original equation to get the value of x, as we did when solving by substitution.
We can still solve by combination even if the variables aren’t lined up so nicely. For example, we can start over and solve the system of equations by making the y‘s cancel, rather than the x‘s. To do that, we can multiply the first equation (1) by the number 2 on both sides:
![]()
Now subtracting (2) from that result gives us:
![]()
![]()
![]()
Solving, we find x = 7. To finish the job, we substitute x = 7 into either of the original equations. If we plug x = 7 into (1), we get:
![]()
![]()
Subtracting 14 from both sides, we get
![]()
And dividing by 3, we find that
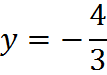
So the solution to the two equations (1) and (2) is:
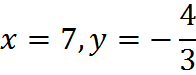
Most people prefer the substitution method to the combination method. However, the combination method will prove much faster on certain questions, so if you don’t consider using it, you are likely to lose time or a correct answer on the Quant section. Furthermore, you want to be comfortable with the concept that equations can be added, since a given equation is after all equal on both sides, since that fact can be useful even when you are not solving a system of linear equations by the combination method.
Practice Questions
Ernesto and His Wife’s Ages:
https://www.gmatfree.com/ernesto-and-his-wifes-ages
Men and Women Assigned to Projects:
https://www.gmatfree.com/men-and-women-assigned-to-projects
A Difference and a Total:
https://www.gmatfree.com/a-difference-and-a-total