Ratio and Proportion

A ratio compares two quantities in terms of multiplication. For example, suppose that there are 10 boys and 15 girls in a classroom. One way, not using ratios, to compare these quantities would be to say that there are 5 more girls than boys in the classroom. To employ a ratio, we say that the ratio of boys to girls is 10 to 15, or 2 to 3. In other words, for every 2 boys in the classroom, there are 3 girls.

Writing a Ratio

You can express a ratio using a colon or a fraction: namely, as

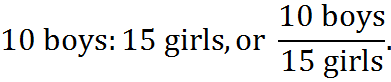
The fraction notation is usually superior for ratios with two elements, but if you have a ratio with three elements, the colon notation is usually superior: for example, 10:15:19.

In the classroom example, many other ratios can be made. The number of boys out of the total number of students is 10/25. The number of girls out of the total number of students is 15/25. And 15/10 is the ratio of the number of girls to the number of boys.

Ratios, being fractions, can sometimes be reduced. For example, the ratio of boys to girls in our hypothetical classroom is 10/15. So, we would be correct if we said that the ratio of boys to girls in our hypothetical classroom is 2:3, or two boys for every 3 girls.

Notice that knowing a ratio doesn’t tell us the actual numbers involved. If the ratio of boys to girls is 2:3 or 2/3, we don’t know whether the actual number of boys and girls is 2 and 3, 10 and 15, or 200 and 300. This fact appears frequently on GMAT questions.

Proportions

A proportion is an equation of two ratios. For example, this is a proportion:

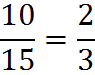
A proportion may contain variables:

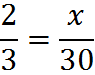
To solve such an equation, we can use cross-multiplication. In the example above, we find 3x = 60, yielding x = 20.

On many GMAT questions, you will be given a ratio, and you will solve by setting up a proportion. For example, a simple GMAT question might state, “The ratio of boys to the total number of boys and girls in a classroom is 2/3. If there are a total of 30 boys and girls in the classroom, how many boys are there?”

In this case, the question has given us a ratio, 2/3. We set up a proportion by finding something that we can set the ratio equal to:

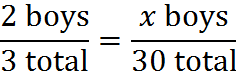
Cross-multiplying, we find that x = 20. There are 20 boys in the classroom.

Examples

1. Is the ratio 4/6 equal to the ratio 12/16?

We can test by cross-multiplying. If the cross-products are equal, then so are the original two ratios. Therefore, we ask:

No, 64 is not equal to 72, so the original ratios are not equal.

2. Solve for x.

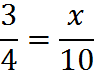
Cross-multiply.

Solve for x by dividing both sides of the equation by 4:

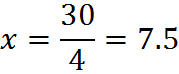
3. Solve for x:

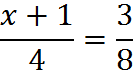
Cross-multiply:

Now, we subtract 8 from both sides:

Divide both sides by 8:

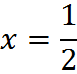
Exercises

Reduce each ratio.

1. 2/10

2. 12/48

3. 3x/9x

Solve each proportion.

4.

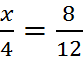
5.

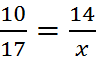
6.

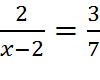
Answers:

1. 1/5

2. 1/4

3. 1/3

4. 8⁄3 = 2.67

5. 23.8

6. 20⁄3 = 6.67

Practice Questions

Ratio of Profits:
https://www.gmatfree.com/ratio-of-profits

Ratios of Marbles:
https://www.gmatfree.com/ratios-of-marbles

Ratios of Children:
https://www.gmatfree.com/ratios-of-children