Radicals

Square Roots

The square root of a number x is that number r which, when squared, becomes x:

Every positive real number has two square roots, one positive and one negative. For example, the two square roots of 25 are 5 and −5. The positive square root is denoted with a radical sign:

Since the square of every real number is a positive real number, negative numbers do not have real square roots (and all numbers on the GMAT are real; GMAT questions do not consider, account for, or include non-real numbers).

Worth emphasizing is that the radical sign indicates a positive number, even though an equation with a squared variable may have a positive or negative solution. For example, the value of

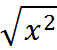
will be positive, even though the equation

has both positive and negative roots, +3 and -3. Note the key difference between these two cases. On the GMAT, the radical sign always indicates the positive square root, but a squared variable has both positive and negative roots.

Cube Roots

A cube root of a number x is a number r whose cube is x:

Every real number x has exactly one real cube root, written,

For example,

and

Simplified Form of a Radical Expression

To reduce a radical expression to simplified form, factor out as many perfect squares as possible from within the radical, and multiply by a form of 1 to remove all radicals from the denominator (if there’s a fraction present).

For example, to write the radical expression

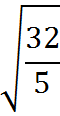
in simplified form, we can proceed as follows. First, look for a perfect square under the square root sign and remove it:

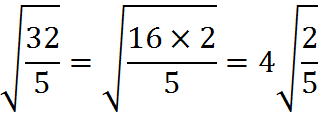
Next, there is a fraction under the radical sign, which we change as follows:

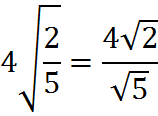
Finally, we remove the radical from the denominator as follows:

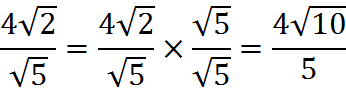
The GMAT does not place special emphasis on the simplified form of a radical expression, but in some questions, you will obtain an answer in non-simplified form and you will have to obtain the simplified form in order to select the correct answer choice.

Roots Other than Square Roots and Cube Roots

The square root and cube root are particular cases of the nth root. The nth root of a number x is a number r which, when raised to the power of n, equals x:

where n is the degree of the root. A root of degree 2 is called a square root and a root of degree 3, a cube root. Roots of higher degree are referred by using ordinal numbers, as in fourth root, twentieth root, etc.

For example: 2 is a square root of 4, since 2 squared is 4. And −2 is also a square root of 4, since the quantity negative 2 squared also is 4.

Roots are treated as special cases of exponentiation, where the exponent is a fraction:

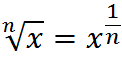
Indeed, the common radical notation is the same as the exponent:

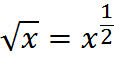
Properties of Roots

Every positive real number has a positive nth root and the rules for operations with such roots obey the following rules:

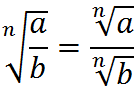
We can convert any expression with radicals into an exponent form:

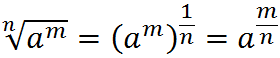
Using the exponent form makes it easier to cancel out powers and roots. We will cover exponent rules in more depth in the next chapter.

Since roots are special cases of exponents, radical rules are essentially exponent rules written with a different notation, the radical symbol.

Practice Questions

Simplifying Radicals:
https://www.gmatfree.com/simplifying-radicals

Summing Radicals:
https://www.gmatfree.com/summing-radicals

Radical and Power:
https://www.gmatfree.com/radical-and-power