Quadrilaterals
Types of Quadrilateral
A quadrilateral is a polygon, a multi-sided closed shape, with four sides. The most obvious quadrilaterals are rectangles and squares. We will need to know a bit more about quadrilaterals for the GMAT, but not much. First, recall that rectangles and squares are both members of a broader category, parallelograms:
- Parallelograms are four-sided polygons (i.e., quadrilaterals) whose opposite sides and angles are equal. The opposite sides are not only equal, but also parallel, hence the name.
- Rectangles and squares are parallelograms, since they have equal facing sides. They both meet an additional criterion, which is that they have all angles of 90 degree. And, finally, a square meets a final condition, which is that it has not only facing sides of equal length, but all four sides of equal length.
- Rhombuses are not defined in the official GMAT language (so you don’t need to know them), but we can clarify the term in case it’s kicking around in your memory. Rhombuses are parallelograms in which all the sides are equal, and opposite angles are equal. Squares are therefore rhombuses, but there are rhombuses that are not squares, such as diamonds with sides of the equal length.
- There are parallelograms that are not rectangles, squares, or rhombuses. We will discuss parallelograms in more detail in the next section.
- Trapezoids are quadrilaterals that have two opposite sides that are parallel. The parallel sides are referred to the upper and lower bases. They are not parallelograms since the other two sides are not parallel to each other. Trapezoids are discussed further below. Trapezoids appear on GMAT questions.
- Finally, irregular quadrilaterals are any quadrilaterals that do not fit into one of the groups above. Irregular quadrilaterals do appear on GMAT questions.
Rectangles and Squares
Before we discuss the other quadrilaterals, here are the basics about rectangles and squares tested on the GMAT. We know the shape below is a rectangle, because it has four right angles (indicated by the square symbol in the angle):
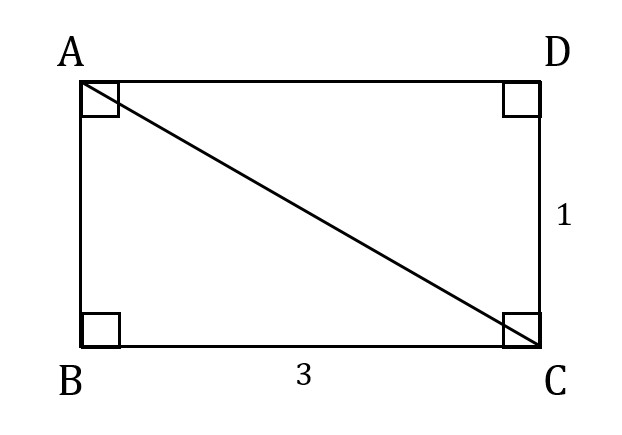
On the GMAT, we cannot assume that a particular angle is a right angle just because it looks like 90 degrees. However, we can sometimes infer that we are dealing with a rectangle without being told every single angle. Since the angles sum to 360 degrees, as they do in any quadrilateral, we can write an equation of the angles:
![]()
If we knew only that angle ABC and angle BCD were both right angles (that is, if we knew less than in the figure above), then the equation would simply be:
![]()
We can’t be certain that we have a rectangle from this information: the final two angles could be right angles or sum to 180 in a different way. However, if three angles are each known to be right angles, then we are left with one equation and one unknown, and we know we are dealing with a rectangle.
In the rectangle above, the length of the diagonal is equal to
![]()
using the Pythagorean Theorem. Every rectangle contains two identical right triangles formed from its sides and its diagonals. And in the case of a square, those two triangles are 45-45-90 triangles.
The area of the rectangle above is
![]()
![]()
and its perimeter is
![]()
![]()
![]()
Practice Questions:
Rectangular Floor:
https://www.gmatfree.com/rectangular-floor/
Equal Rectangular Areas:
https://www.gmatfree.com/equal-rectangular-areas
Overlapping Frames:
https://www.gmatfree.com/overlapping-frames/