Quadratic Equations

A quadratic equation is one which includes a squared variable (and no term with a higher exponent). In general, a quadratic equation can be expressed in the form

As we have seen, all linear equations represent lines in the coordinate system. Quadratic equations have their own characteristic shape, a parabola:

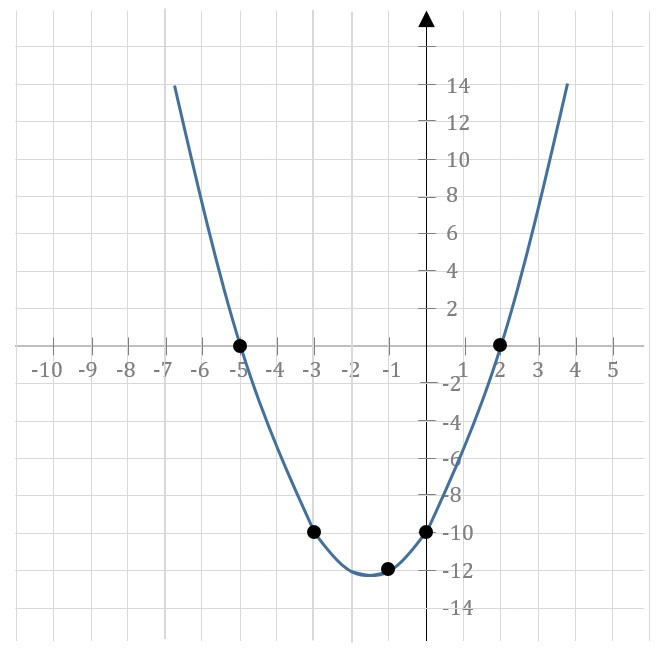
The graph of the quadratic equation

can be sketched approximately by hand
by identifying various point values

Most GMAT equations with quadratic equations are purely algebraic and don’t involve graphing. However, just as you can do with linear equations, you can test or plot individual points on the graph of a quadratic equation one point at a time, by testing x and y values. For example, you can see on the graph above that the graph of the quadratic equation contains the point (2,0). You could confirm this by substituting x = 2 into the equation and obtaining

so y = 0, as expected.

The two points at which the parabola crosses the y-axis are significant. If you are given a quadratic equation and you need to solve for x, there will be either 0, 1, or 2 solutions – the points on the graph where y = 0.

Solving a Quadratic by Factoring

Many GMAT test takers think immediately of the quadratic formula (discussed below) when presented with a quadratic equation. The quadratic formula is not the most important way to solve a quadratic equation on the GMAT. A GMAT test taker usually can break 700 or even 750 without using the quadratic formula even once, but you are almost certain to use another method for quadratics: solving a quadratic by factoring.

To solve a quadratic equation, manipulate it so that you have a quadratic expression equal to zero and then factor that expression. To put that in formal terms: it may be possible to express a quadratic equation

as a product

Let’s use factoring to solve this quadratic equation:

To factor it, we must get it into the form:

As we can confirm by FOILing, the numbers “?” and “??” must multiply together to give -3, the value of c in the un-factored quadratic. And while they aren’t necessarily integers, we should start with integers. Either 3 and -1, or -3 and 1. But we also need to get the x coefficient correct (here, b = 2). So, we also need our two factors of c to add together to make b. And (3) + (-1) = 2. So, we have found our unknowns: they are 3 and -1. Let’s fill them in.

To check that we have factored correctly, we could expand the parentheses back out with FOIL to get the expression we started with:

Back to the factored expression: we know that in an equation the left side is always equal to the right side. And in this case the right side of the equation is 0, so from that we can conclude the term (x + 3)(x – 1) must equal to zero as well. And that means that either (x + 3) or (x – 1) must equal zero. That’s key: when we factor a quadratic that is equal to zero, one term or the other must equal zero. Not convinced? Remember (x + 3) and (x – 1) are just numbers. Can you find two non-zero numbers which multiply to make zero?

Let’s write that algebraically:

Thus, there are two different solutions to the same equation. This is the case for all quadratic equations. We say that this quadratic equation has two distinct (real) roots.

Here is another example. In this case, we can factor simply by removing an x, so we don’t have to reverse-FOIL:

Last Resort: The Quadratic Formula

Sometimes the roots (solutions) of a quadratic equation cannot be obtained by simple factoring. In such a case, we can solve the equation by using the quadratic formula. Note that this situation is rarely seen on the GMAT: you should always try factoring first. In fact, you can safely ignore this subsection until your Quant performance is very strong. Because of the adaptive nature of the test (see the online course unit “The GMAT Exam” at www.gmatfree.com/the-gmat-exam/ for more on that), you won’t otherwise see a question that tests this knowledge.

Given that a quadratic is in the form,

the quadratic formula gives the two roots as:

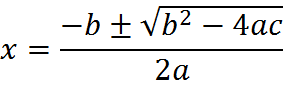
This formula gives us the roots of the quadratic (as equal to x) when we put in the values of a, b, and c in a particular quadratic equation. For example, for

we can see right from the coefficients that a = 2, b = 8, and c =2. Plugging these values into the quadratic formula, we get:

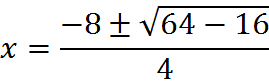
There is a plus/minus in the solution, so we have two possibilities. Either:

or

There is a special part of the quadratic formula, the portion in the numerator:

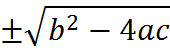
The fact that this expression is “plus or minus” in the formula is why there are typically two roots: one root is generated from the plus and the other from the minus. So, the reason that some quadratic equations have only one root is that this term can be zero. For those quadratics,

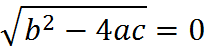
and therefore

This expression is known as the “discriminant” of a quadratic:

The discriminant allows us to determine whether a quadratic has zero, 1 or 2 roots. For example, if you get a quadratic like this,

you know that it has only a single distinct root, because

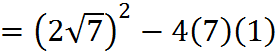
Since the discriminant is zero, there is only a single root to the equation. In this case, the single root happens to be

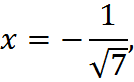
as you can find by completing the formula.

And you can actually do something similar with a quadratic like this:

The discriminant is negative, because

Since the discriminant is negative, the square root of the discriminant will not give any real number. This quadratic does not have any real solutions. (It has imaginary roots, but imaginary numbers are outside the scope of the GMAT.)

Practice Questions

Other Solution of a Quadratic Equation:
https://www.gmatfree.com/other-solution-of-a-quadratic-equation

Two Quadratic Equations:
https://www.gmatfree.com/two-quadratic-equations

Quadratic Equation:
https://www.gmatfree.com/quadratic-equation