Percentages

The word “percent” means “out of 100” or “per 100.” The word “per” can be thought of as denoting the bar of a fraction. A percentage is a number or ratio expressed as a fraction of 100. It is expressed with the percent sign, “%”, or the abbreviation “pct.”

For example, 4% is the same as the decimal value 0.04 or the fraction 4/100 (which could be reduced to 1/25):

Another example:

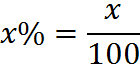
If you’re dealing with a number that is not expressed as a percentage – if there is no % symbol – then, to convert it to a percentage, multiply by 100 and add the % symbol:

Since the percent symbol, %, stands for “per one hundred,” when we multiply by 100 and add a percent symbol, we are in fact merely multiplying by a form of the number 1 (the “chameleon” has appeared again).

Percentages are used to express how large or small one quantity is relative to another quantity. The first quantity usually represents a part of, or a change in, the second quantity. For example, an increase of $0.15 on a price of $2.50 is an increase by a fraction of

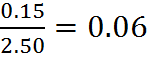
Expressed as a percentage, this is therefore a 6% increase.

The base of a percentage change is the starting value. Many errors occur from using the wrong base in a percentage calculation.

Percentages are usually used to express values between zero and one. However, it is possible to express any ratio as a percentage; for example, 111% is 1.11 and −35% is −0.35.

Calculating a Percent Value

The percent value is computed by multiplying the numeric value of the ratio by 100. For example, to find 50 apples as a percentage of 1250 apples, first compute the ratio 50/1250 = 0.04, and then multiply by 100 to obtain 4%.

To calculate a percentage of a percentage, convert both percentages to fractions or decimals and multiply them. For example, 50% of 40% is:

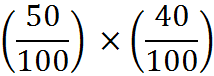
Another, often easier, way to take a percent of a percent is to turn one into a fraction. For example, 40% of 50% is the same as 40% times one half, or one half of 40%, which is 20%.

Dividing by 100 and using the percent sign at the same time is mathematically allowed but may be the result of an error. For example,

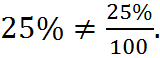
On the left side, we have

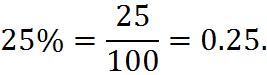
On the right side, we have

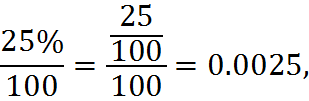
which is 100 times smaller.

Whenever we talk about a percentage, it is important to specify what it is relative to – the total that corresponds to 100%. For example: in a certain college 60% of all students are female, and 10% of all students are business majors. If 5% of female students are business majors, what percentage of business majors are female?

To answer that question, we know that 60% or 3/5 of all students are female and that 5% of these are business majors, so we conclude that

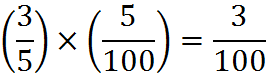
Therefore, 3% of all students are female business majors. And we already know that the 10% of all students, male and female, are business majors. Therefore, the percentage of business majors who are female is:

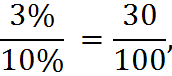
or: 30% of all business majors are female.

We can simplify the preceding computation through a handy GMAT trick. When you have to compute a percentage of an unknown total value, you can let the unknown total value equal 100 and work with whole numbers. In this case, we don’t know the total number of students–that’s the unknown total value. If we let that unknown total equal 100, then the number of females is 60 and the number of business majors is 10. Furthermore, 5% of females are business majors–that means 3 females are business majors, and the percentage of business majors who are female is 3/10, or 30%. Note that the digits of this computation are identical to those in the calculation above, but since we have selected the number 100 for the unknown total, we can do the computation with whole numbers.

Examples of Percentage Increase and Decrease

Sometimes, due to inconsistent usage, it is not always clear from the context what a percentage is relative to. When speaking of a percent change in a quantity, the standard interpretation is that the change is relative to the initial value of that quantity. For example, if an item is initially priced at $200 and the price rises 10% (an increase of $20), the new price will be $220. Note that this final price is 110% of the initial price (100% + 10% = 110%).

Some other examples of percent changes:

• An increase of 100% in a quantity means that the final amount is 200% of the initial amount (100% of initial + 100% of increase = 200% of initial); the quantity has doubled.
• An increase of 800% means the final amount is 9 times the original.
• A decrease of 60% means the final amount is 40% of the original.
• A decrease of 100% means the final amount is zero.

In general, a change of x percent in a quantity results in a final amount that is (100 + x)% percent of the original amount, or the quantity (1 + 0.01x) times the original amount. If the original amount is V₁, then the final amount is V₂ is:

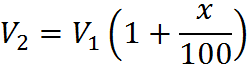
For example, if x = 7, the final quantity is 107% of the original or 1.07 times the original. We’ll now cover this more precisely with the percentage change formula.

Percentage Change Formula

We just discussed a number of examples of percentage change, a way to express a change between the old value of something and a new one.

For example, if a house is worth $100,000 today, and after a year its value goes up to $110,000, the percentage change of its value can be expressed as

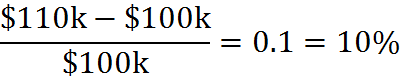
The value of the house has increased by 10%.

More generally, if V₁ represents the old value and V₂ the new one, then the percentage change, x, is

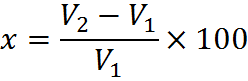
Note that, although the value of the house has units (U.S. dollars), the units cancel out in the fraction. The percentage change has no units; it is unitless and will be unitless for any percentage change.

When you are talking about the change in a percentage, the formula is the same. If a bank were to raise the interest rate on a savings account from 3% to 4%, the relative change in the interest rate is:

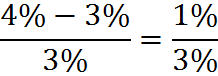
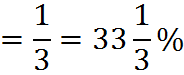
Note that the percentage change from 3% to 4% is not 1% – it is approximately 33.3%. The difference of 1% is the absolute change, not the percent change.

If we want to talk about the absolute change in this case, to avoid confusion, we should say that the interest rate increased by 1 percentage point. In general, the term “percentage points” indicates an absolute change or difference of percentages, while the percent sign or the word “percentage” refers to the relative change or difference. On the GMAT, questions will not typically discuss “percentage points” with that term, but they will switch between absolute and relative differences.

Percentages of Different Bases

If a store has an item for a regular price of $100, marks it 20% off, and then charges 6% sales tax on the reduced price, what is the total amount paid for the item?

First, calculate 20% of $100. That’s $20. We then subtract that $20 from the original price of $100 to get a reduced price of $80.

Now we add in the sales tax. Here’s where the tricky part comes in; what is the base? That is, do we pay 6% tax on the original $100 price or on the reduced $80 price? We have been told by the question that we pay tax on the reduced sales price, so $80 is the base. Thus, we multiply $80 by 0.06 to get $4.80 and add that to $80 to get $84.80 for a final price.

Notice that even though we took off 20% and then added back in 6%, this is not the same as taking off 14%, since the 20% and the 6% figures each had a different base. If the 6% sales tax was computed based on the original, full price, however, then both percentages would have the same base and the total reduction in price would, indeed, be 14%, and would bring the price down from $100 to $86.

We have percentages of different bases when we have compound percentages–percentages of percentages. We’ll now discuss compounding percentages in more detail.

Compounding Percentages

Percent changes do not add when applied sequentially. For example, if the 10% increase in price considered earlier (on the $200 item, raising its price to $220) is followed by a 10% decrease in the price (a decrease of $22), the final price will be $198, not the original price of $200. The reason for the apparent discrepancy is that the two percent changes (+10% and −10%) are measured relative to different bases ($200 and $220, respectively), as we have just discussed, and thus the changes do not “cancel out.”

We have already seen that, for a single percentage change x, if the original amount is V₁, then the final amount is V₂ is:

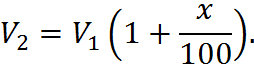
In general, if an increase of x percent on an initial amount of V₁ is followed by a decrease of x percent, the final amount V₂ is

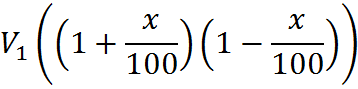
This is not a new formula; it simply the previous formula applied twice, or substituted into itself. We simply applied the percent-change equation to get a so-called “final value,” and then again to get the actually final value.

Using the difference of squares (reviewed in the algebra section of this book), we get:

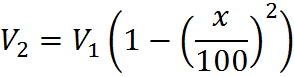
Thus the net change is an overall decrease by x percent of x percent (the square of the original percent change when expressed as a decimal number). Thus, in the above example, after an increase and decrease of x = 10 percent, the final amount, $198, was 10% of 10%, or 1%, less than the initial amount of $200.

This can be expanded for a case in which you do not have the same percent change. If the initial percent change is x, the second percent change is y, then the final amount V₂ is

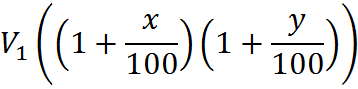
Equivalence of Formulas

You don’t need to memorize each of these formulas individually. This is the original formula for percentage change, given old and new values:

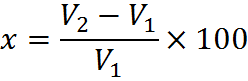
And secondly, as we discussed, given the first value V₁ and a percent change x, the formula for final value is

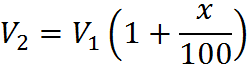
These are the same equation. We can see these by starting with the second equation, expanding the term on the right:

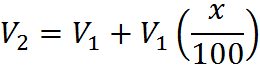
Then subtract V₁ from both sides:

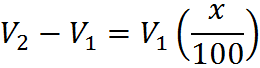
Then divide by V₁:

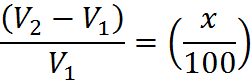
Then multiply both sides by 100 and switch right and left sides:

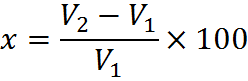
And we are now back to the first formula, the one for percent change. This single formula is all we have used in these calculations. You can gain some speed and reduce errors by memorizing the different versions above, but keep in mind that they are all manipulations of the same thing.

Practice Questions

Percent Decrease in Value:
https://www.gmatfree.com/percent-decrease-in-value

Revenue from Sweaters:
https://www.gmatfree.com/revenue-from-sweaters

Teachers Aged 30+:
https://www.gmatfree.com/teachers-aged-30