Math With Units
On the GMAT, as in the real world, many numbers have units associated with them. When we are dealing with two numbers that are expressed in units, if the units are the same, we can add or subtract normally. However, if the units are different, then we can add or subtract only if the units can be converted into the same units.
For example:
![]()
![]()
Some units are different but can be converted into a common unit. For example,
![]()
![]()
![]()
We can perform the following addition only if we can convert apples into U.S. currency:
![]()
On the GMAT, you will encounter situations in which you use standard unit conversion (e.g. 1 foot = 12 inches):
![]()
![]()
![]()
The GMAT generally does not require you to be familiar with any particular unit system other than the basic time units of seconds, minutes, hours, days, weeks, months, and years. Both US units and the metric system are used, but when you have to perform a conversion of units, the units will be given to you.
An example in which unit conversion is required:
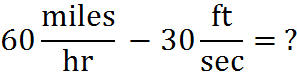
To perform this subtraction, we need to get the two fractions into the same units. The first term is equal to
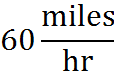
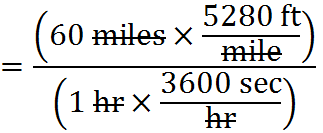
Both multiplications occurring in this fraction are allowed because they involve multiplying by a form of 1. For example, 3600 seconds is 1 hour, so the fraction multiplied by 1 hr. in the denominator is simply a multiple of 1 that changes units.
Putting that fraction back in the expression we have to evaluate, we have:
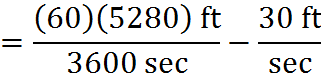
At this point, the units in both fractions are the same. We are done converting units. This method is called unit cancellation or dimensional analysis.
We can make an important side observation. At this point in this particular computation, we can cancel not only units here, but also factors. The fraction on the left need not be computed as it is; we can simplify it. Two factors of 10 on the top and the bottom of that fraction cancel, giving us:
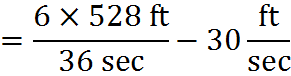
Furthermore, the numerator and denominator both have a factor of 6, which we can cancel:
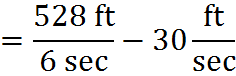
What we have to compute has been simplified radically! Rather than multiply 60 and 5,280 and divide the product by 3,600, we have only a single, simpler division to do. We can finish by dividing 528 by 6, using long division, to get:
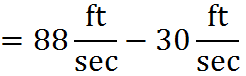
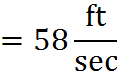
You will be able to perform many simplifications like this one on the GMAT. Look for opportunities to cancel factors whenever you are dealing with fractions.
Multiplication and Division
When multiplying or dividing numbers with units, the units are also multiplied or divided.
Here are examples using the same base units:
![]()
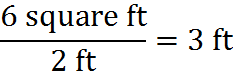
Although various squared and cubed units are meaningful in physics, the only squared and cubed units you’re likely to encounter on the GMAT are squared and cubed lengths, corresponding to area and volume, respectively.
For example, in the case of a rectangular solid:
![]()
![]()
It is also possible to multiply or divide a number with units by a scalar (a unitless number):
![]()
![]()
Since exponents represent multiplication, exponent operations apply to the units just as multiplication does.
Examples:
![]()
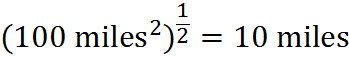
In the first case, we calculated that a cube 2 feet long on each side has a volume of 8 cubic feet. In the second case, we calculated that a square plot of 100 square miles of land is 10 miles long on each side.
Practice Questions
Converting Units:
https://www.gmatfree.com/converting-units
Distance to the Moon:
https://www.gmatfree.com/distance-to-the-moon
Visible Stars in the Night Sky:
https://www.gmatfree.com/visible-stars-in-the-night-sky