Long Multiplication

Multiplication “by hand” is necessary on the GMAT. You can often use tricks to simplify calculations, but you’ll have to write out some. It’s a good habit to leave space along the side of your scratch paper – which will be your noteboard, on the GMAT – for long multiplication and long division. On the Quantitative section of the GMAT, you will not be allowed the use of a calculator. For the Integrated Reasoning section, you’ll have a built-in calculator, but the Quant section is far more important, as that section goes into your Total Score of 200-800.

Long Multiplication: The Method

To multiply two multi-digit numbers:

1. Right-align the two numbers. Write the two numbers you are multiplying, one under the other, with the numbers aligned at their rightmost digits. People usually put the number with fewer digits (32, in this case) on the bottom. For example, if we want to multiply 832 and 32, we line them up like this:

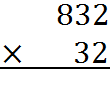
2. Multiply the top number by the bottom units digit. Next, multiply the entire number on the top line by the units digit on the bottom. Write the result, aligned to the right, under the multiplication bar.

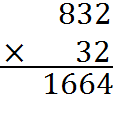
3. Multiply by the bottom tens digit, adding a zero. Next, multiply the entire number on the top line by just the tens digit on the bottom. Since you are multiplying by a tens digit, you add a zero (or an empty space) to your result and you put it under the first result:

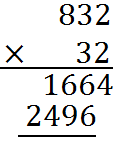
4. Continue multiplying by higher digits and adding zeroes until you are done with the digits of the smaller number you are multiplying. In this case, we are already done multiplying by 32, because 32 has only three digits.

5.  Add the partial results to get the final product. In this case, we have two numbers to add.

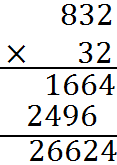
6.  Add commas and a decimal point to your answer, as needed. We’ll talk more about decimal points, in a moment. In this example, we don’t need a decimal point, although we may insert a comma. And we have our result: 832 times 32 equals 26,624.

Finally, we can check our answer by estimating. The number 832 is roughly 800, and the number 32 is roughly 30. And 800 times 30 is 24,000. That product is in the ballpark of 26,624, so our estimate indicates that we have not accidentally added or omitted a zero somewhere.

Long Multiplication: Adding the Zeroes

There is nothing magical about the fact that we add a zero with each line of the multiplications by digits that we do in the course of long multiplication. We can see this from our example:

Here, we can think of 32 as 30 + 2:

And, as we will discuss in the introductory algebra sections later in this book, we can multiply out this expression:

The parentheses in this last above are not required and have just been added for emphasis. More on that in the section on Order of Operations. The second term, 832 times 2, is the beginning of our long multiplication, the first partial product:

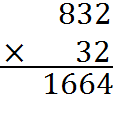
And the term 832 times 30 is just the line that comes under it. So it really does have an extra zero, because when we multiply by the digit 3 in the long multiplication, we are truly, you could say, multiplying by 30.

Long Multiplication: Example

This example uses long multiplication to multiply 23,958,233 and 5,830 and arrive at the product, 139,676,498,390.

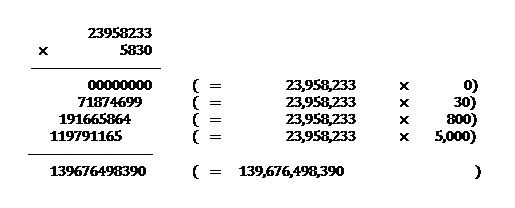
It’s easy to practice multiplying numbers. You can write down any old two numbers, picking them randomly or from a receipt from the last time you bought coffee, and try multiplying them. You can check the product on your phone or by entering the computation into the search box on Google (if you enter a computation into Google, it will give you the answer).

Long Multiplication with Decimal Places

You can multiply two decimal numbers by ignoring the decimal points and adding the decimal point back into your result. To add the decimal point back in, count the number of digits to the right of the decimal points of the two original numbers; the total of the two counts indicates the number of digits that will be present in the product to the right of the decimal point.

For example, if you have one number with two digits after the decimal point and another number with one digit after the decimal point, their product will have three digits after the decimal point. That’s the case in this multiplication:

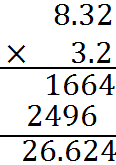
Notice that this multiplication is identical to our first example apart from the addition of decimal places. Decimal places have no impact on how the digits multiply. So, to multiply 8.32 and 3.2, we start with the multiplication 832 by 32. At the end, we add back in the total number of missing decimal places – three – to get our final result.

Again, we can estimate as a way of double-checking our product. The number 8.32 is about 8, and the number 3.2 is about 3. So their product should be roughly 24. Indeed, the product, 26 plus change, is pretty close to 24.