Inequalities
An inequality is an expression that compares the relative sizes of numbers, expressions, points, lines, or curves. Unlike equations, in which both sides are always equal, inequalities have unequal sides.
There are four main inequality signs:
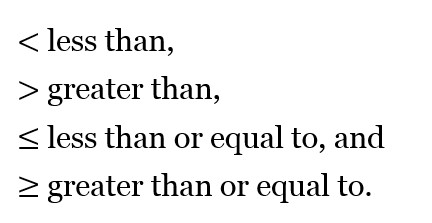
Note that x > y and y < x convey the same information.
If you become confused with which sign means less than and greater than, it is useful to remember that the inequality signs always point to the smaller number. The point is small and the open part is larger, and they point to the smaller and larger parts, respectively. Or, to use the sophisticated technique I employ: the inequality sign is like a hungry alligator’s mouth opening to eat the larger number.
Solving Linear Inequalities
Inequalities have some similarity to equations. For example, instead of the equation,
![]()
we could have the inequality:
![]()
We can solve this inequality as we would solve an equation: by taking actions on both sides. Subtracting 4 from both sides, we get
![]()
Then, dividing both sides by 2, we get
![]()
We have solved the inequality. In this case, x may be any number greater than 1.
An inequality can be manipulated and therefore solved almost just like an equation. One difference is that the inequality, once solved, gives a range of values; no more exact solution is possible. Another key difference is that there is a critical rule for inequalities when you multiply or divide by a negative number…
Multiplying or Dividing by a Negative Number
Even a quant-heavy engineer can fall prey to this trap on the GMAT. When multiplying or dividing by a negative number, you must change the direction of the inequality sign.
For example, look at the inequality 10 > 5. This is a correct statement, since 10 is greater than 5. Now, if we were to multiply both sides by -1, we would get:
![]() .
.
This is incorrect, since -10 is actually less than -5; it is left of -5 on the number line. By reversing the inequality sign, we now have the correct inequality:
![]() .
.
This fact will likely earn you 10 points on the GMAT: when multiplying or dividing by a negative number, you must change the direction of the inequality sign.
Combining Inequalities
When you are working with any inequality, but certainly more than one inequality, you should draw a number line and sketch the information you have on it. This technique will give you all the power you need when combining inequalities.
When you have two inequalities, there are three possible cases:
Case I: The inequalities point in opposite directions and overlap. There are some cases where two inequalities can be combined into one. For example, we are given the following statements about the height of a door x:
![]()
and
![]()
When inequalities point in opposite directions and overlap, they can be combined to define a line segment on the number line. In this example, the inequalities can be combined to give
![]()
Case II: The inequalities point in the same direction. Another case when they can be combined is when one inequality essentially consumes the other on the number line. For example, if we know these statements:
![]()
![]()
then the first inequality is completely contained within the second one, and the two inequalities, when taken together, tell us simply that
![]()
Case III: The inequalities point in opposite directions and do not overlap. Inequalities cannot be combined if they have no overlap. This situation could arise if there is a contradiction. For example, if we are given the inequalities
![]()
![]()
and we are told that both are true, we are being told something impossible. The two regions do not overlap, so x cannot be in both of them.
On the other hand, it might be the case that one or the other is true: either x is in this first region on the number line or in this second region on the number line. We don’t know which of the two regions x is in, from that information alone, although we don’t know that it’s not 1.93, for example, since that value is on the little segment between the two regions.
Practice Questions
Integers Within An Inequality:
https://www.gmatfree.com/integers-within-an-inequality
Quadratic Inequality:
https://www.gmatfree.com/quadratic-inequality