Graphing a Linear Equation
As we’ve discussed, a linear equation is one that has variables that are not multiplied by each other or taken to any exponent.
 Two linear equations
Two linear equations
A common form of a linear equation in the two variables x and y is
![]()
where m is the slope of the line and b is the y-intercept, which is the y coordinate of the location where line crosses the y axis. This can be seen by letting x = 0, which immediately gives y = b. It may be helpful to think about this in terms of y = b + mx, where the line passes through the point (0, b) and extends left and right with a slope of m.
Slope
Slope is the measure of how much a line moves up or down relative to how much it moves left to right.
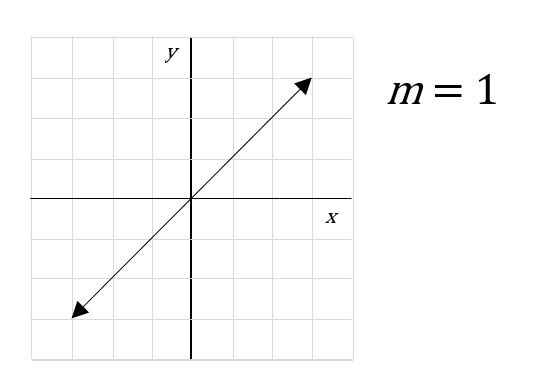 In other words, slope is the “rise” over the “run,” or the steepness of a line. In the figure above, the slope of the line is
In other words, slope is the “rise” over the “run,” or the steepness of a line. In the figure above, the slope of the line is
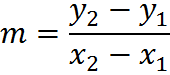
It is also expressed as
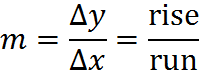
where the Greek uppercase letter delta represents the change in a value.
If a line goes up from left to right, then the slope is positive. For example, a slope of 3/4 exhibits a rise of 3 for each run of 4 to the right, so it slopes up. Both numbers in the slope are either negative or positive in order to have a positive slope.
If a line goes down from left to right, then the slope is negative. For example, a slope of -3/4 exhibits “rise” of -3 for each run of 4 to the right, so it slopes downward. Only one number in the slope can be negative for a line to have a negative slope.
A horizontal line has a slope of zero. A vertical line has an undefined slope, since division by zero is forbidden. Parallel lines are those that have the same slope. Perpendicular lines have slopes that are negative reciprocals, such as 3/4 and -4/3.
Determining Slope
For the most part, finding slope when given some information is not difficult. Simply take the linear equation y = mx + b and replace the variable with whatever information you know, and solve.
For example, let’s find the slope between the points (1,4) and (4,8):
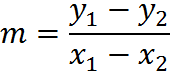
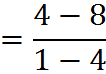
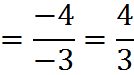
Note that it doesn’t matter which point you call “1” and which you call “2.” You can try switching the points and you will get the same slope, 4/3.
Infinite Solutions
A single linear equation of two variables has infinite solutions. In fact, each of the points on the line is a possible solution. However, if we have two distinct equations of lines, then we can find a single solution. We can see this by returning to the example from above:
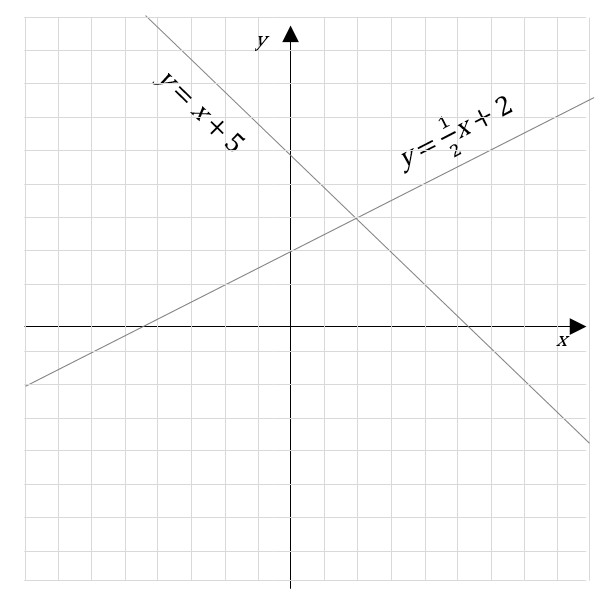
 Any two lines have a mutual solution at their intersection
Any two lines have a mutual solution at their intersection
If we have only one of the two lines, y = –x + 5, then then x and y could have any values that create a coordinate pair on the line. But if we are given both lines – in other words, we are told both lines are true – then x and y must have values that create a coordinate pair for a point that is on both lines. As you can see in the graph, there is only one such possibility: the point at which the lines cross. In the next section, we’ll see how to find this solution.
Practice Questions
Slope of a Line:
https://www.gmatfree.com/slope-of-a-line
Equation of a Line:
https://www.gmatfree.com/equation-of-a-line