Word Problems
The GMAT requires you to know a few formulas that are used in word problems. These formulas are best practiced by doing realistic questions, so we’ll cover them quickly here and you can move on to the questions.
Word problems tend to be heavy on ratios. For this reason, the manipulation of ratios in different contexts is arguably the most useful skill on the Quantitative section.
Rate Problems
The GMAT uses the term “rate” for what we would call the “speed equation”:
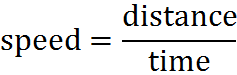
The use of the term “rate” highlights that we are talking about a type of equation that does not necessarily involve speed or motion. Then, we can write the same equation as:
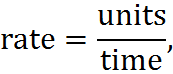
where the units in question could be miles, for example – in which case we are talking about speed – but they could also be, say, units of production in a factory process. And, indeed, many GMAT questions use rates other than speed.
The rate formula is simple, but it can be transformed and applied in a variety of ways. One useful fact is that, since we have a single equation with three quantities in it, knowing any two will allow us to determine the third.
Combining Rates
The GMAT features many questions in which rates are additive. In other words, Machine A might output a units per second, and Machine B might output b units per second. Together, they output a + b units per second. This obvious notion is the backbone of many somewhat tricky GMAT questions. Keep an eye out for questions in which rates are combined. When they are, write out the rates in the units of (units/time) and add them that way, and then rearrange to identify whatever you need to solve for.
Absorbing and applying that small fact will make at least one or two questions of moderate difficulty trivially easy when you sit for the GMAT.
For example, if it takes Machine C t seconds to make a widget, and Machine D s seconds to make a widget, how many widgets can they make in 30 seconds? To solve, we write and add the rates:
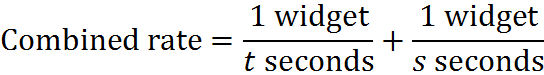
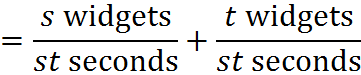
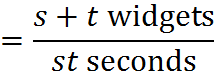
That’s the combined rate. To find out how much it generates in 30 seconds, we manipulate to get 30 in the denominator:
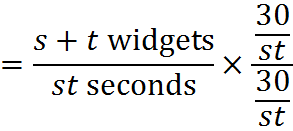
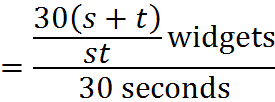
Therefore, the machines working together produce
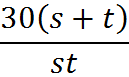
widgets in 30 seconds. All we did here was keep track of the units, add the rates, and then work with the units again to get what we were looking for. We’ll see this further in the practice questions.
Time for Two Combined Rates
There is a popular formula for solving simpler rate questions. It is covered by the above rule (write rates and add, then format), but many GMAT test takers gravitate to it, so let’s cover it.
Notice that, when we found the rate for Machine C and Machine D above, we get the following combined rate:
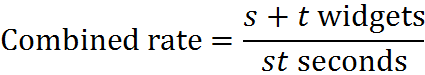
Altering the question above, suppose now that we want to find the time to produce one widget. Again, we can multiply by a form of 1,
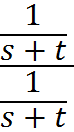
to get
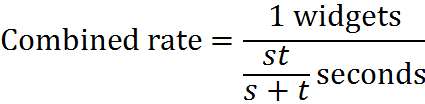
With our eye on the denominator of this equation, we can conclude that, if one machine takes s time to do a task and another machine takes t time to do a task, the time for them working together T is:
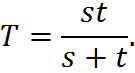
This equation is expedient for the particular case that it covers. However, if you remember only this formula, you will likely get stuck when you run into situations that are slightly more complicated. So, above all, remember to approach combined rate questions by writing the rates with units and adding those rates.
Practice Questions
Difference in Distances Over Time:
https://www.gmatfree.com/difference-in-distances-over-time
Time to Turn Around:
https://www.gmatfree.com/time-to-turn-around
Machines and Combined Rate:
https://www.gmatfree.com/machines-and-combined-rate
Mixture of Spices:
https://www.gmatfree.com/mixture-of-spices