Triangles

Triangles are the geometrical subject on the GMAT about which you must know the most. There are numerous properties of triangles tested on the GMAT, and they can be combined in myriad ways (and with other geometric facts). The good news is that, once you know triangles well for the GMAT, you have learned the bulk of geometry required for the test.

Properties of All Triangles

The interior angles of a triangle always add up to 180 degrees. If you make one angle bigger, another angle will become smaller:

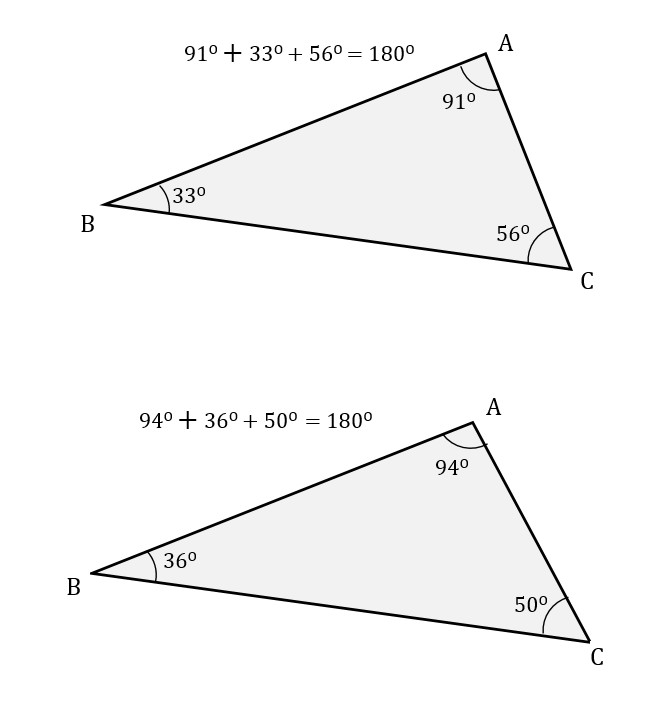
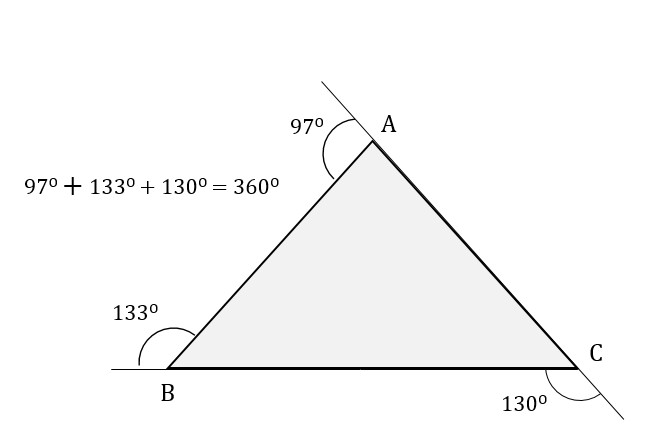
The exterior angles of a triangle always add up to 360 degrees:

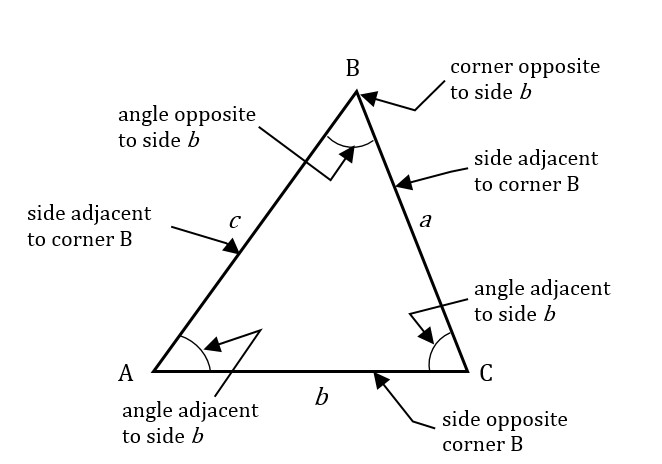
In every triangle, the shortest side is always opposite the smallest interior angle. The longest side is always opposite the largest interior angle. “Opposite” means that the side does not touch the point of the angle on either end.

Equilateral triangles must have three angles of 60 degrees each, and all triangles with three 60 degree angles are equilateral. Similarly, if a triangle has two equal angles, it has two equal sides, and vice versa.

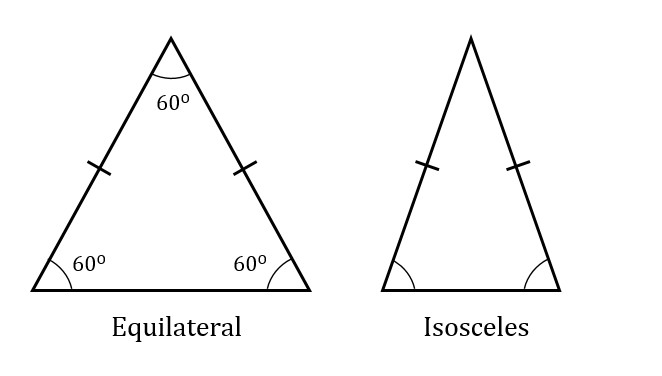
The fact that you can make an inference about the sides based on the angles, or vice versa, is frequently tested on the GMAT. For example, you may see on a particular question that two sides of a triangle are of equal length, and then, with that knowledge, you’ll infer that the facing angles are of equal measure.

Aside from equilateral and isosceles triangles, there is another special type of triangle on the GMAT, the right triangle, which will discuss at length in the next section.

Area of a Triangle

The area of a triangle is half the base times the height. The “base” of the triangle is any side you choose to make the base. The height is then the distance measured at right angles from the base to the apex, the furthermost point of the triangle not on the base. The diagrams below show how the height and base are measured.

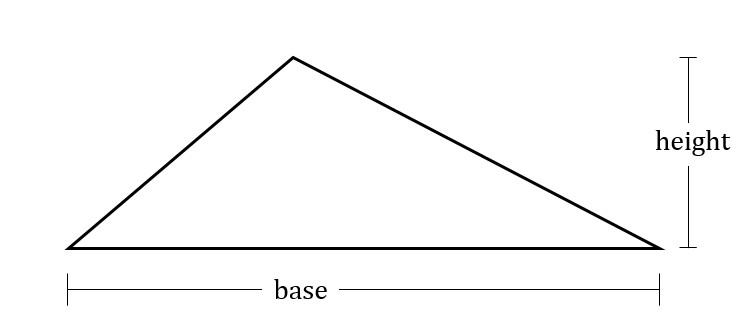
The base and height of a triangle

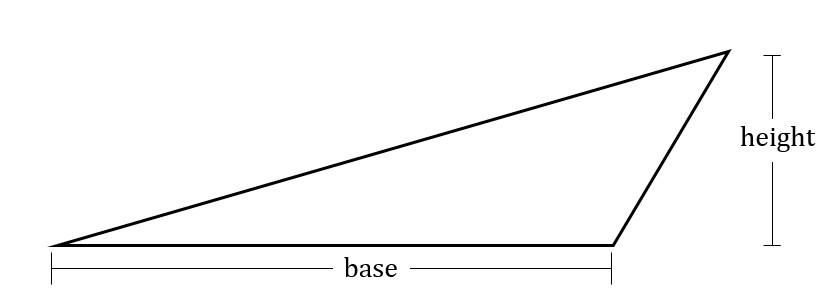Another triangle with the same base and height

Given a valid base-height pair, the area of the triangle is given by:

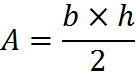
Any side of a triangle can be considered a “base” in order to compute area, as long as a valid height is associated with that base. For this reason, when you want to calculate the area of a triangle on the GMAT, you should not think to yourself that you are looking for “the” height and “the” base, but rather, “a valid base-height pair.” That knowledge will quite possibly earn you an additional question when you sit for the exam.

Practice Questions

Triangle in the Coordinate Plane:
https://www.gmatfree.com/triangle-in-the-coordinate-plane

Interior and Exterior Angles of Triangle:
https://www.gmatfree.com/interior-and-exterior-angles-of-triangle

Angles of a Triangle:
https://www.gmatfree.com/angles-of-a-triangle/