Interest

Simple Interest

Simple interest is calculated only on the principal – the original amount of an investment. Consequently, the interest earned by an investment according to simple interest is the same in one given time period as in any other time period. And that means that, in order to calculate the total amount earned in a simple interest situation, all you need to do is determine the amount of interest earned in a unit of time and multiply that amount by the number of units of time that have passed.

Simple interest is:

where r is the period interest rate, P the principal (the initial amount), and t is the time elapsed.

For example, imagine that an investment has an initial value of $2500 and that the simple interest rate is 12.99% per year. The interest earned by the end of 3 months is,

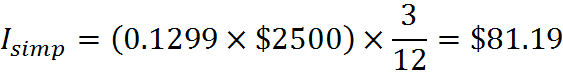
and at that time the total value of the investment is $2500 + $81.19 = $2581.19.

The total value of the investment is equal to the initial principal plus the amount of interest earned. Therefore, the total value V is:

Factoring out P, we obtain:

Compound Interest

Compound interest is earned not only on principal (as in the case of simple interest) but also on all interest that has already been earned. It’s like having a growing amount of principal, although technically the “principal” is once and forever equal to the amount of the initial investment. Because the body of investment that earns interest grows over time, the amount that is earned in a given time period grows over time, even though the interest rate itself does not change. This is why such investments balloon in value over time, and why, out in the real world, people advise you to invest your money (in the world of finance, compound interest is the norm).

For example, here’s the value of an investment of $1,000 that earns 20% compound interest annually:

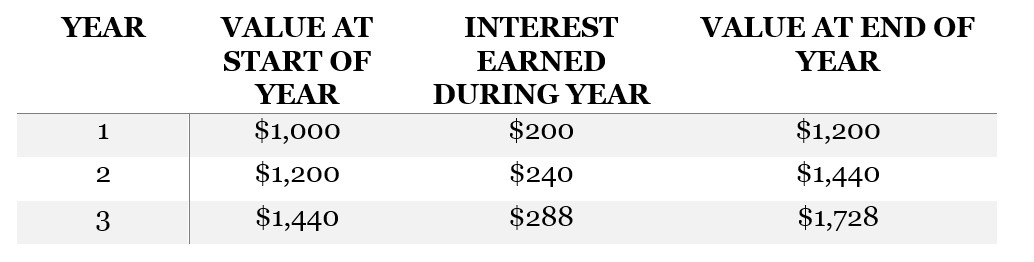
Notice how the amount of interest earned (listed in the middle column) increases each year. If this investment were at 20% simple interest, the middle column would be $200 for each year.

To define a compound interest rate, the interest rate and the compounding frequency must be specified. In the example above, the interest rate compounds “annually,” so the interest of 20% must be calculated and applied on a per-year basis.

Suppose the investment above were compounded semiannually, not annually. “Semi” means “half,” as in “semicircle,” so in this investment, interest is earned every 6 months. If it’s a “20% annual interest rate, compounded semiannually,” then we must apply 10% each six months:

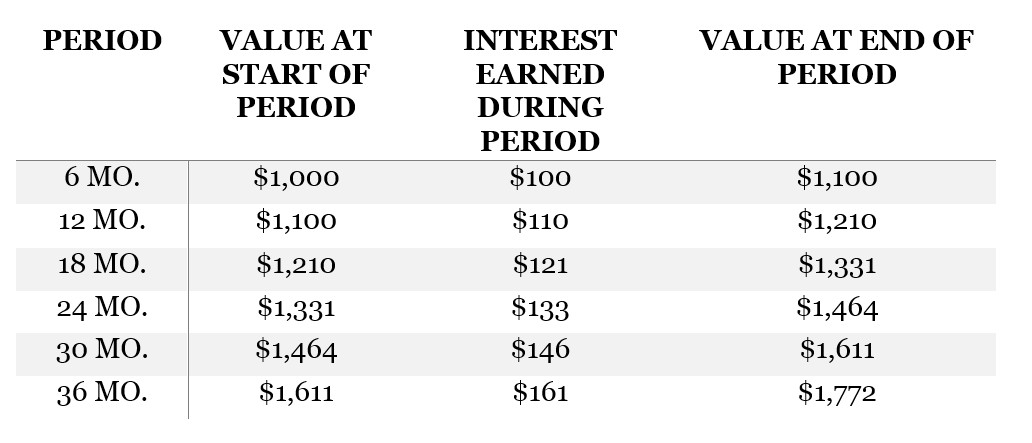
Over three years, the effect of compounding semiannually is similar to that of compounding annually, but the investment grows a little faster, because interest makes it back into the pile faster to accumulate further interest.

When we deal with simple interest, as above, it’s equally easy to compute the interest that has been accumulated by a given time (I_simp) and total value of an investment (V) at that time. In the case of compound interest, it’s easier to work with the value of the investment, V. The formula for calculating V is:

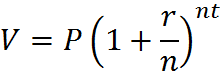
where:

• V = value after t periods
• P = principal amount (initial investment)
• r = interest rate per period
• n = number of times the interest is compounded per period
• t = number of periods the money is borrowed for

For example, the final value in the first compounding example is:

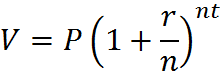
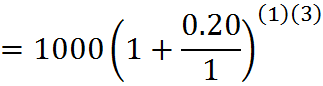
And in the second compounding example it’s:

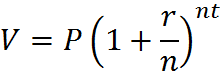
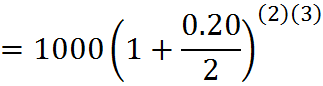
Comparing with the tables above, you can see that r/n is the interest applied in the middle column of each table, and the exponent nt is equal to the number of rows in the table, the number of compoundings.

To play around with different numbers and increase your level of comfort with this formula, you can search for an online “compound interest calculator” to confirm that you are setting up the equation properly for different cases.

Something the GMAT doesn’t expect you to memorize, but which we can work through an example, is finding an equivalent annually compounded rate for the second case. In other words, what annually compounded interest rate, call it r, would be equivalent to a 20% annual rate compounded semiannually? This unknown r, since it is equivalent, leads to an equal final value of the investment; therefore,

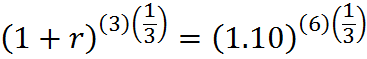
We have figured out, in other words, that an investment at a 20% annual interest rate compounded semiannually increases in value identically to one at a 21% annual interest rate compounded annually. Financial institutions typically employ such calculations. For example, a credit card company might compound the interest charged on a balance on a monthly basis but convey the interest rate to customers as an effective annual rate, an APR.

The Rule of 72

The “rule of 72” give an estimate how long an annually compounded investment takes to double in value. This rule is not a required piece of knowledge for the GMAT, but it can be handy to check your work or to solve specific situations. To use the rule, you divide 72 by the interest rate, and that’s an estimate for the number of years it will take to double.

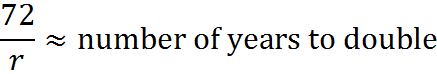
So, an investment at 8% (compounded annually) will take approximately 72/8 = 9 years to double. If you bump up that rate to 9% (compounded annually), it will naturally double a little faster – in about 72/9 = 8 years. An investment at a measly 2% (compounded annually) will double in about 72/2 = 36 years, while an investment at the rather unrealistic rate of 72% (compounded annually) will double in 72/72 = 1 year… wait, that’s not right! An investment of 100%, not 72%, will double an investment in one year. Indeed, the rule of 72 gives only an estimate; it’s more accurate for lower interest rates, which are what we tend to work with, anyway.

Practice Questions

Compound Interest:
https://www.gmatfree.com/compound-interest

Pat’s Investment:
https://www.gmatfree.com/pats-investment

Two Investments:
https://www.gmatfree.com/two-investments