The Coordinate Plane

The coordinate plane (also called the Cartesian plane, after Descartes of, “I think, therefore, I am,” fame) is a uniform regular grid used for graphing. Many algebraic expressions lend themselves to graphical analysis.

The location of a point in the coordinate plane is graphed by indexing two numerical values (coordinates) along two perpendicular number lines. For example, here is a plot of the point (5,3), which has an x-value of 5 and a y-value of 3:

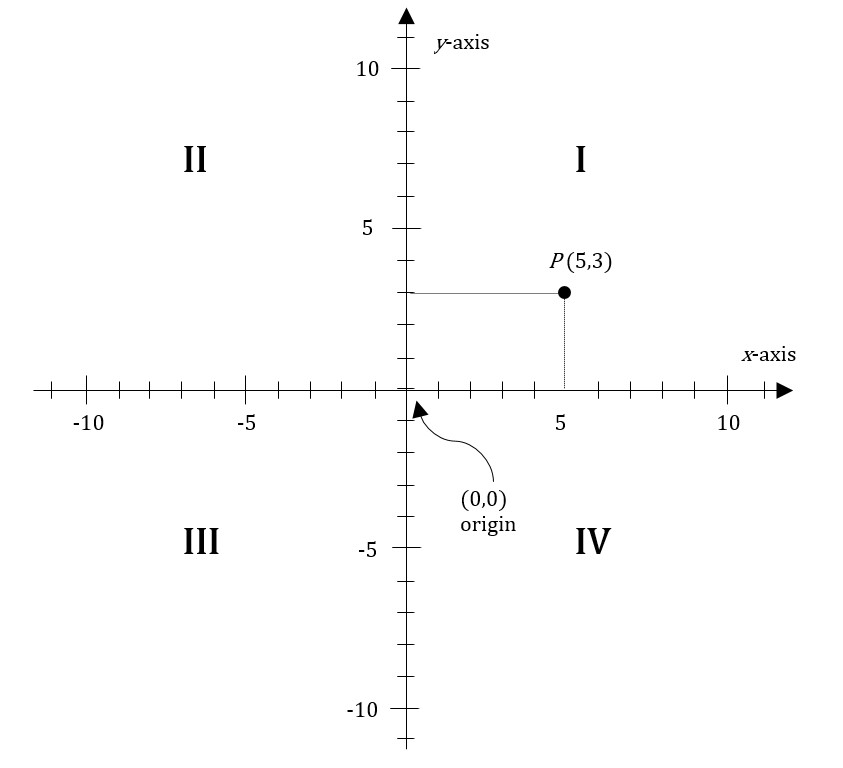We choose the values or ordinates for points on the Cartesian plane using two perpendicular numbered axes. By convention the point where the two axes cross is labeled as 0 on each axis, making the ordinate for their intersection a special point called the origin and labeled (0,0).

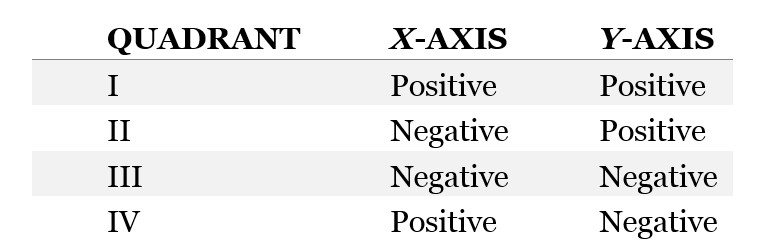
The axes extend infinitely in both directions. The four quadrants of the system are labeled I, II, III, IV. The GMAT will not require you to remember which quadrant has which number, but it will in some questions ask you to compare points or lines in different quadrants. For example, notice that quadrant I is the only quadrant in which both x and y are positive.

Plotting Functions in the Coordinate Plane

A mathematical function gives you a single output for a single input. You can think of a function as what’s sometimes called a “black box”: regardless of what happens on the inside, the box spits out something, given an input. Here is a conceptual depiction of such a black box with the mathematical symbols that we commonly use:

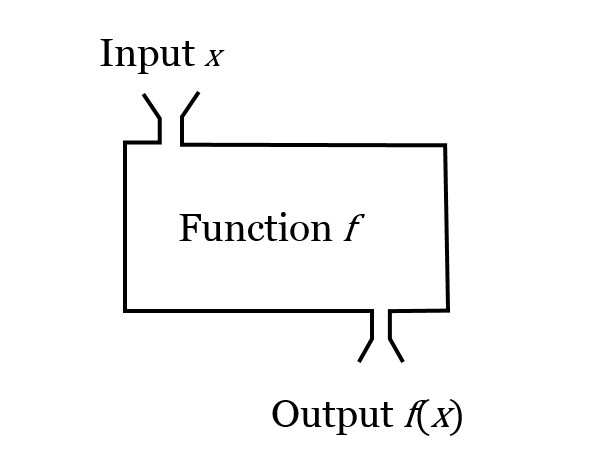Mathematical functions are similar to equations. Note that, in this diagram, the output is labeled as f(x), which is pronounced “f of x.” That label is expressing the fact that the output of the function is “a function of x.” But we can often think of f(x) simply as y. For example, the function,

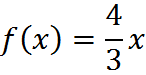
means that, if we plug in 1, we get

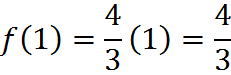
If we plug in 3, we get

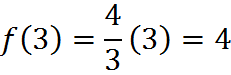
That latter example is shown here in the coordinate plane:

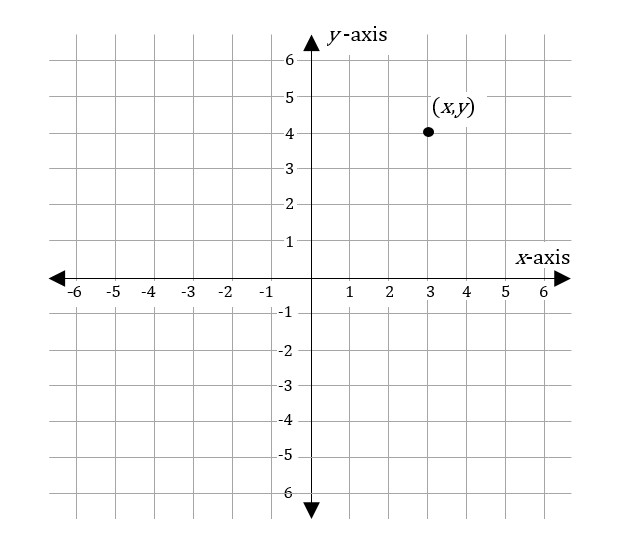
When you have a graph in the coordinate plane, you can think of it as a function. The x axis (or independent axis) represents all of the possible inputs into the function. And each of the points on the graph gives the function’s output for that input; the input 3 gives the output 4, so the graph contains the point (3,4).

Any equation of x and y can be thought of as a function in the coordinate plane. The function f(x) = 4x is essentially just a different notation for y = 4x. And any such equation can be graphed on the plane, as we’ll see in the next section, focusing on linear equations. Furthermore, the variables in question don’t have to be named x and y in order for us to use the coordinate plane or to draw a line. For example, if you have an equation of two variables r and s, you can think of r as x and s as y and graph the line of that equation accordingly.

Distance in the Coordinate Plane

To find the distance between any two points in the coordinate plane that aren’t already along a horizontal or vertical line, you can use the Pythagorean Theorem, which we review later in the section on triangles. Namely, the distance between the two points is the hypotenuse of the right triangle; the difference between the x coordinates is the length of the base of the triangle, and the difference between the y coordinates is the length of the height of the triangle.

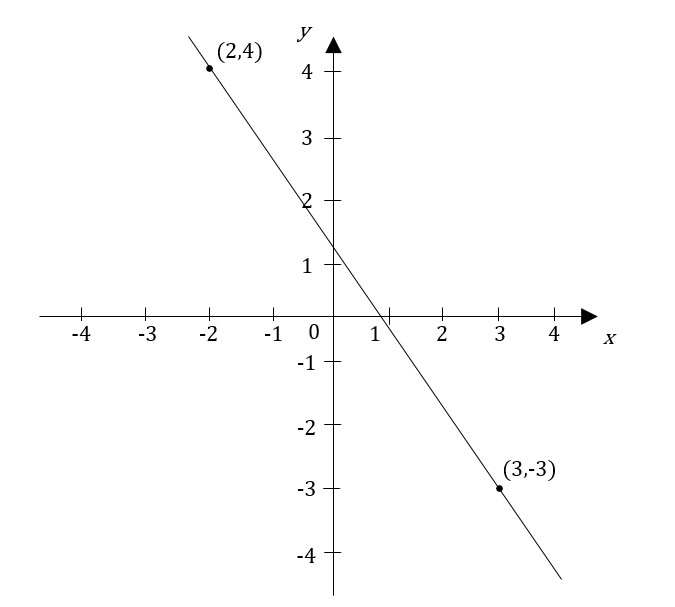Therefore, to compute a distance, the Pythagorean Theorem,

can be rewritten as

Taking the square of both sides, and switching the sides, we have an equation for the distance D:

In this equation, we compute the difference in x values and in y values to find the distance D. For example, in the figure above, the triangle is of dimensions 5 and 7, so the distance is

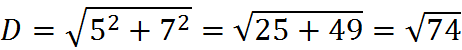
which we can estimate to be between 8 and 9, since the square root of 74 is between the square root of 64, which is 8, and the square root of 81, which is 9.

Practice Questions

Points in Coordinate Plane:
https://www.gmatfree.com/points-in-coordinate-plane

Bisecting a Line:
https://www.gmatfree.com/bisecting-a-line