Working with Algebra

Algebra is math with variables. A variable, such as the classic choice of notation, x, is a quantity whose value is unknown. While a variable is often given the symbol x, any letter can be used, and there is not automatically a significance to the selection of the letter.

(You may be wondering, “If this is algebra, what have we been doing until now?” When there are no variables involved, what we are doing is called arithmetic. Being able to recognize the difference is not important to solving any GMAT question, though it may help to organize your GMAT preparation.)

The “sentences” of algebra are equations. An equation is a mathematical statement that two things are equal. There is an equals sign = between two expressions. 2 + 2 = 4 is an example of an equation, as well as 3 + x = 7.

Similarly, algebraic expressions are like phrases, or sentence fragments. 2 + 2 is an example of an expression. An expression does not correspond to a complete sentence in the language of algebra.

You will need to understand and recognize the difference between an equation and an expression for the GMAT. For example, many questions are solved using the n variables, n equations rule, which we will discuss soon. To use that rule, you need to count up the equations you have at hand in a question. If you have an expression and count it as an equation, that could lead to an incorrect answer.

Less critical words are “term” and “coefficient.”  A term is any variable, constant or a product of variables or constants which are separated by a plus or a minus sign. In the expression 3x + 4xy – 2y, the separate terms are 3x, 4xy, and -2y. A coefficient is the constant part of a term which multiplies the variable part of the term. For example, in 4xy, the coefficient is 4.

Collecting Like Terms

When collecting like terms, you add and subtract all terms that can be added and subtracted – all the terms with the same exact variable (or variables multiplied together). For example, when we collect like terms in this expression,

we get:

Multiplication

We indicate that variables are multiplied together by writing them next to each other. For example, a multiplied by b is written as ab.

When digits are present or extra clarity is desired, parentheses are used to indicate that things are multiplied together. For example, if we want to write the product of 389, 5, and x, we can write (389)(5)(x). Most likely, in such an instance we are about to multiply 389 and 5, but by writing the prior step first we can keep track of our work and don’t attempt to force ourselves to do too much in our head.

Notice that

is potentially confusing. If you write such an expression on your noteboard, you could end up mistaking a multiplication sign that you’ve written for a variable, or vice versa. For this reason, it’s best on your noteboard to write the multiplication of algebraic expressions with parentheses, such as (x)(x) or (3)(5).

As in addition and subtraction, in multiplication, you keep like terms together. For example:

becomes:

which can be simplified as:

Expansion of Parentheses: FOIL

Suppose we have to multiply out the following expression:

This process is usually summed up by the mnemonic FOIL:

·     F=> start with the product of the First terms in the parentheses:

·     O=>add the product of the Outside or outermost terms in the parentheses:

·     I=> add the product of the Inside terms or innermost in the parentheses:

·     L=> add the product of the Last terms in the parentheses:

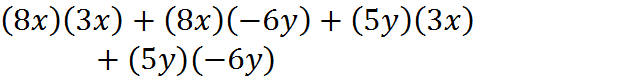
Then, once you have collected terms, you are done.

Typically, as in this case, two of the terms can be combined:

And we have the final, expanded expression.

FOIL is Just the Distributive Property

While FOIL is a good mnemonic, understanding why it works will help on more difficult GMAT questions. Here is another way to think about the expansion of our original expression,

Actually, scratch that… Let’s ignore that expression for a moment and start with this simpler one:

To expand this expression, we multiply each term on the inside of the parentheses by 8x. This is a manifestation of the so-called distributive property:

Here’s another simple expansion:

You expand that one, too, by multiplying both terms on the inside by 5y. If you consider these two simpler expansions added together,

you have two terms with a common factor of (3x – 6y). Taking out that common factor gives us our original expression of interest, (8x + 5y) (3x – 6y). In other words, (8x + 5y) (3x – 6y) is the same as multiplying 8x by (3x – 6y), and then adding the result of 5y multiplied by (3x – 6y). Each term on the left gets multiplied by each of the terms on the right once. Moreover, the quantities in parentheses could be reversed, as (3x – 6y) (8x + 5y), and we’d get the same result. So, really all that’s happening in the expansion is that each of the four terms is multiplied by each of the other three terms exactly once, and all those products are summed up. FOIL is just a mnemonic to stay organized in this process.

Factoring

Sometimes, expressions can be rewritten as the product of their factors. This is called factoring (or factorising, in some countries). For example, to factor

you must first find a common factor between the two terms. The number 5 is a common factor between the two terms. Now you divide the whole expression by 5, leaving you with 2x + 3y. Place 2x + 3y inside the parentheses and the factor, 5, outside. The factored expression is

You can multiply out the expression to confirm that you get the original expression and hence that you have factored correctly.

Let’s factor another expression,

This expression has a common factor x. The factored form of this expression is

Now that we’ve discussed expanding and factoring, you may be wondering, “If expanding and factoring are opposite actions, what’s the point here? How am I supposed to know on a GMAT question whether to put something in factored or expanded form?” A correct and somewhat careful answer to that question is that expanding and factoring are simply algebraic tools at your disposal, and it’s your job on a particular question to decide which tool you need to use. For example, to isolate a variable such as x on one side of an equation, you may have to factor or expand multiple times. A cruder but very practical answer for the GMAT is the following: if you see an opportunity to factor or to expand an expression on a GMAT question, it’s usually a good idea. Quite often, if you see that you can factor or expand, and you try it, you are close to the answer and the rest of the question will become clear to you.

Later, we will discuss an important application of factoring, solving quadratic equations.

Difference of Squares

There is an important, aptly named special case of factoring called the “difference of squares.” If you expand this expression using FOIL:

you will find that it multiplies out to give the expression

The process here is identical to FOIL above, but we get a simpler result because the Outer term xy ends up canceling with the Inner term –yx, leaving just the squared terms.

When most people see two expressions in parentheses multiplied together, such as (a – b)(a + b), they usually think to expand it. But when presented with an opportunity to go in the other direction, many people will miss it. Spotting the opportunity to split a difference of squares into factors will lead straight to the answer on some GMAT questions. The difference of squares sometimes appears on questions in hidden formats, so you want to keep it in the back of your head and look for it when complex quantities are multiplied or squared terms are present.