Fractions
A fraction consists of one quantity divided by another quantity. The fraction “three divided by five” or “three over five” or “three fifths” can be written as
![]()
Writing in vertical notation with a horizontal bar keeps computations with the fraction organized, since we often perform actions across the top and bottom of a fraction.
Numerator and Denominator
The first quantity, the number on top of the fraction, is called the numerator. The other number, on the bottom, is called the denominator. For example, in the fraction 3/5, the numerator is 3 and the denominator is 5.
You can think of the denominator as the “type” of a fraction – or “denomination” of a fraction, much how a $5 bill and a $10 bill are of different denominations.
Multiplying Fractions
To multiply two fractions, multiply the numerators to get the new numerator, and multiply the denominators to get the new denominator. That’s it!
For instance,
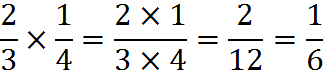
Dividing Fractions
To divide one fraction by another one, flip the numerator and denominator of the second fraction and then multiply the two fractions. The flipped-over fraction is called the reciprocal.
For instance,
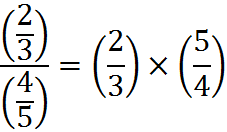
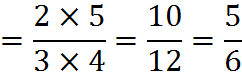
Adding Fractions
To add or subtract two fractions, you first need to manipulate the two fractions so that they have the same denominator.
To see why a common denominator is necessary, consider adding the value of coins using fractions. A U.S. quarter is worth a quarter of a dollar, or $1/4. For that reason, 13 quarters are worth $13/4, and if we add three more quarters, the total worth is $16/4; that is, we simply add 13+3 in the numerator.
But if we throw in three U.S. dimes, we can’t simply add 3 to the numerator of the fraction 13/4. Dimes and quarters are worth a different amount – or, to put it differently, they are each worth a different fraction of a single dollar. To add up the value of quarters and dimes, we need to express them in a common denominator, such as cents, and then each quarter is worth 25/100, and each dime is worth 10/100. With that common denominator, the values of the two coins have been expressed in such a way that they can be compared to each other or added.
That’s why we need a common denominator whenever we add two fractions: failing to use one would be like counting quarters and nickels as equal in worth.
One way to get a common denominator is to multiply the numerator and denominator of each fraction by the denominator of the other.
For instance,
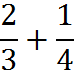
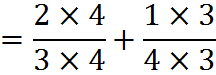
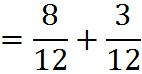
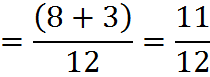
Another way to get a common denominator is to calculate the lowest common multiple (LCM) of the denominators, as we have discussed.
Reducing Fractions
Sometimes on the GMAT you will need to rewrite a fraction in smaller numbers, while also keeping the value of the fraction the same. This is known as simplifying, or reducing to lowest terms. You’ll typically do this on a Problem Solving question once you have computed an answer and need to match it with one of the answer choices, which are all expressed in lowest terms.
To reiterate, reducing fractions is essentially replacing your original fraction with another one of equal value, called an equivalent fraction. Below are a few examples of equivalent fractions.
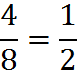
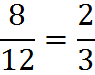
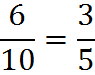
When the fraction 4/8 is reduced to lowest terms, it becomes 1/2. This example fits our common sense. A fraction is in its lowest terms when both the numerator and denominator cannot be divided evenly by any number other than one.
Division Method
To reduce a fraction to lowest terms, you must divide the numerator and denominator by the largest whole number that divides evenly into both. For example, to reduce the fraction 3/9 to lowest terms, divide the numerator (3) and denominator (9) by three:
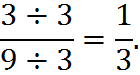
If it’s not obvious what’s the greatest number that can be divided into both numerator and denominator, try dividing the numerator and denominator by any common factor. Repeat this process until you’re convinced the fraction is in lowest terms.
Example:
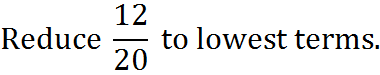
In this problem, the largest whole number is difficult to see, so we first divide the numerator and denominator by two, as shown:
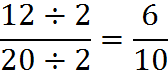
Next divide by two again:
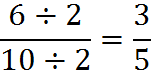
There are no whole numbers left which can divide evenly into 3/5, so we have found the lowest terms.
Another example: let’s reduce 18/24 to lowest terms. To do this, we divide the numerator and denominator by six, as shown:
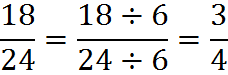
Another example: We’ll reduce 112/126 to lowest terms.
The largest whole number that goes into 112 and 126 may not be immediately apparent. So, first we can divide the numerator and denominator by two:
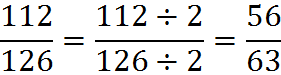
Now we can see that 7 is a common factor between numerator and denominator:
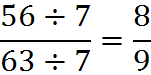
Therefore, 112/126 reduced to lowest terms is 8/9.
Greatest Common Factor Method
The second method of simplifying fractions involves finding the greatest common factor between the numerator and the denominator. We do this by breaking up both the numerator and the denominator into their prime factors:
![]()
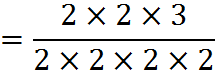
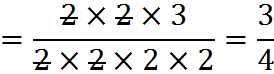
As the strikethroughs above indicate, we divide the common 2’s out of the fraction. (Recall that each 2/2 is just multiplying by 1; that’s why they cancel.) We are left with one 2 in the denominator.
Another example:
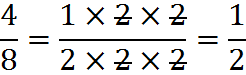
Raising Fractions to Higher Terms
To raise a fraction to higher terms is to rewrite it in larger numbers while keeping the fraction equivalent to the original in value. For example, we can write the fraction 2/5 in higher terms:
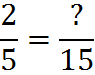
First, ask yourself “what number multiplied by 5 equals 15?” That number is 3:
![]()
So we must multiply the numerator by the same number, 3, to get the missing numerator on the right:
![]()
Therefore,
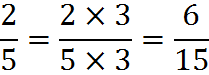
Usually, you’ll raise a fraction to higher terms so that it has a common denominator with another fraction, so that the two fractions can be compared, added, or subtracted.
Fractions Expressing the Number 1, The “Chameleon”
Notice that, above, we converted a fraction by dividing both top and bottom of the fraction by two:
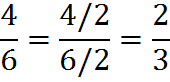
You may have wondered why this is a legal mathematical operation. It’s a legal operation because we are, in fact, simply multiplying a fraction by 1:
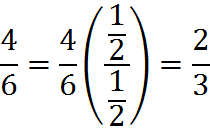
The fraction 1/2 over 1/2 is simply 1. Since it’s just 1, when we multiply the fraction 4/6 by it, the fraction 4/6 doesn’t change in value, only in format.
So we can multiply a fraction by anything over anything, such as
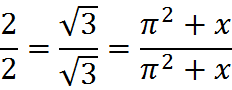
because these fractions are all equal to 1. Since the number 1 can take on countless different forms in this fashion, a former teacher of mine called it the “chameleon” in honor of the color-changing reptile of that name.
This technique is critical to manipulating fractions: the primary way to “reformat” fractions is to multiply by a form of 1, “something” over “something”… in other words, to use the chameleon.
Note that multiplying by 1 differs from working with equations. As we’ll review when we discuss equations, you can perform an action to one side of an equation if you perform the action to the other side. But that rule only applies when you have an equation with two sides and an equal sign. You can use multiplying by 1 anywhere – even when you have a simple fraction or expression and not a full equation – since, once again, multiplying by 1 doesn’t change the value of whatever you’re dealing with.
Mixed fractions
“Mixed fractions,” such as
![]()
contain a portion expressed as an integer and a portion expressed as a fraction. A mixed fraction can be thought of a single number or as a sum of the two parts – for example, as 1 plus 3/5. We are used to thinking in terms of mixed fractions, but they are not easy to work with in mathematics.
The best way to compute the following,
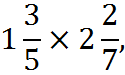
is to convert the mixed fractions into fractions made up of a single numerator and single denominator (without any integer portion). To do this conversion, we first convert the whole numbers into fractions.
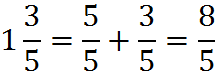
and
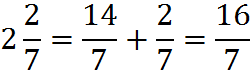
Now we can multiply the fractions:
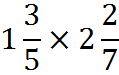
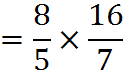
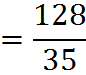
We have our result. Often, we’ll want to convert the result back into a mixed fraction from its current form, which is called an “improper fraction.” We’ll cover how to do that now.
Improper Fractions
When the numerator of a fraction is greater than or equal to the denominator, it’s called an improper fraction. For example, the fractions
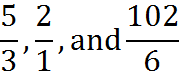
are improper fractions.
All improper fractions are greater than 1. With the proper fraction 6/6, for example, the value of the fraction is 1. When the numerator is increased – whether to 7 or to 102 – the fraction increases in value and will be greater than 1.
As we have seen in the previous section, despite the word “improper,” improper fractions are not bad. It is easier to add, subtract, multiply, or divide two improper fractions than two mixed fractions. So you generally want improper fractions, at least while you are working through a problem. Then, at the end of a GMAT question, you will typically have to convert an improper fraction to a mixed fraction in order to match an answer choice (although you won’t always have to, as answer choices may be in the form of an improper fraction).
To convert an improper fraction into a mixed fraction, perform the division indicated by the fraction bar. For example:

To perform the division indicated by the fraction, we divide 13 by 2. You can use long division to obtain the quotient and the remainder. The division 13/2 gives 6 with a remainder of 1.
We have the whole number part of the answer; it’s 6. To form the fractional part of the answer, we use the remainder (which is 1, in this case) as the numerator and the original denominator (which is 2, in this case) as the denominator. Hence,
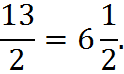
In our example from the previous section, we got the following improper fraction as our answer:
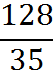
To convert this fraction into a mixed form, we perform the division. The number 35 goes into 128 a maximum of 3 times, as we can find from long division. And the remainder of that division is 23. Therefore,
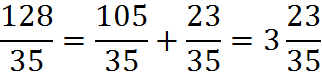
As you can see from this example, in a mixed fraction, the numerator of the fractional component – 23, here – represents the remainder when we perform the division expressed by the improper fraction – 128 divided by 35.
Working with fractions is essential to solving GMAT questions. Many easier Quant questions will give you fractions to evaluate, and many more difficult Quant questions, such as rate questions, are word problems that are solved with fractions. Keep practicing until you feel completely comfortable manipulating fractions and you are their master!
Practice Questions
Subtracting Compound Fractions:
https://www.gmatfree.com/subtracting-compound-fractions
Fractions, Decimals and Denominators:
https://www.gmatfree.com/fractions-decimals-and-denominators
Estimating Sum of Fractions:
https://www.gmatfree.com/estimating-sum-of-fractions
Fraction Subtraction:
https://www.gmatfree.com/fraction-subtraction