Decimals
Decimals are basically fractions expressed in a different format, without a denominator. For example, 0.4 can be thought of as a fraction:
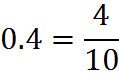
In this case and in every case, when we convert a decimal into a fraction, the denominator is a power of ten – that is, 10, or 100, or 1000 and so on. In fact, position of the decimal point in decimal form corresponds to the power of ten of the denominator in fractional form. In the example above, the decimal is before the “tenth” place in decimal form, so the denominator in the fractional form is 10.
Place Values / Digits of a Decimal Number
GMAT questions sometimes refer to the individual digits or place values of a decimal. Know this terminology:
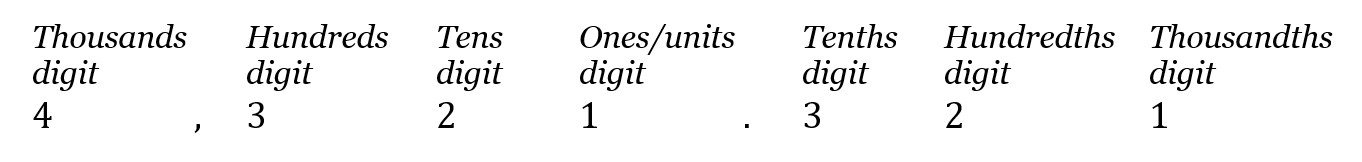
In this number, for example, the “thousands” digit is 4. The terms are sensible, given that a decimal such as 0.321 can be written as a sum of fractions:
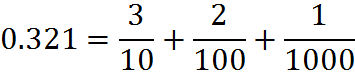
You can see how the notation for the place values makes sense. For example, in the example above, 1 is the “thousandths” digit, because it’s the numerator over 1,000 in the expression of 0.321 as a sum of fractions. Note the importance of not confusing “thousands” with “thousandths,” and so on.
Adding Decimal Numbers
Add decimal numbers much the same way you would add integers. Line up decimal points, and then proceed to add each column and carry at the top. The decimal point in the answer should line up with all of the others. Here is an example:
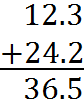
Since you line up the decimal points, sometimes one decimal portion is missing digits on the right. The missing digits are zeroes. For example,
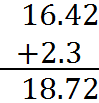
Subtracting Decimal Numbers
Subtract as you would whole numbers, but remember to follow all the rules from addition of decimals.
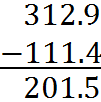
Converting Fractions to Decimal Numbers
To convert a fraction to a decimal number, use long division (discussed earlier). Namely, divide the numerator by the denominator.
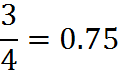
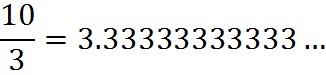
This will, on the GMAT, sometimes require writing out long division on your noteboard.
Converting Decimal Numbers to Fractions
As we saw above, any decimal number can be expressed as a sum of fractions, one fraction per digit of the decimal number:
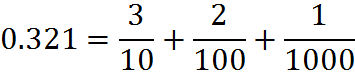
You can use this property to convert any decimal into a fraction. The furthest decimal point indicates what the denominator will be. In this case, the largest denominator is 1,000, so this decimal can be expressed as a single fraction:
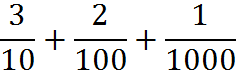
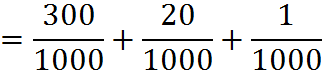
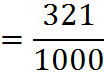
Repeating and Terminating Decimals
A repeating decimal is a decimal that is infinite, such as the 3.33… in the example above. The threes just keep repeating. Instead of writing many 3’s, you can draw a line above the number that is repeating.
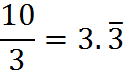
When there are multiple digits repeating, such as in 0.232323, we draw a line over the entire block of repeating digits.
![]()
A terminating decimal is a decimal that ends at one point and does not go on forever. For example, 1.25 has no repeating digits; all the digits after 5 are zeroes and hence are not written.
Multiplying Decimal Numbers
Multiplying decimals is similar to multiplying integers. In fact, one perfectly fine way to multiply decimals is to use the long multiplication method covered near the beginning of this book. As discussed in that section, to multiply decimals using long multiplication, you take the decimal points out at first, multiply, and put the decimal point back in after you have multiplied.
Another way to multiply decimals is to factor out powers of 10. For example, to multiply 0.6 and 0.75, we can factor out powers of 10 to make them both whole numbers:
![]()
![]()
This last line represents four numbers that are multiplied, so they can be multiplied in any order. We can group the first terms in one product, and the second terms in another:
![]()
![]()
Then insert the decimal point into a corresponding power of ten. The previous line is equivalent to:
![]()
![]()
![]()
![]()
You might have noticed a point of similarity between this method and the long multiplication method. When multiplying decimals by long multiplication, we ignore the decimals at first and then put them in at the end. In the example we’ve just looked at, we factored out powers of ten (which move the decimal point) at first and then put the factors of ten back in at the end. Both methods really involve the same mathematics, just with a different appearance.
Dividing Decimal Numbers
Dividing decimal numbers is similar to multiplying them. First, make both decimal numbers have the same multiple of a power of ten.
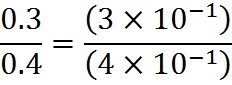
Then divide the first terms together, and the second terms.
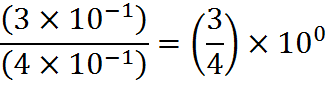
Then insert the decimal point into a corresponding power of ten.
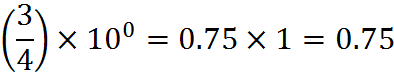
Alternatively, you can make the numbers integers (if the decimal is finite) and perform a simple division.
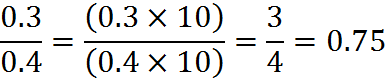
Converting Repeating Decimals to Fractions
Given a repeating decimal, it is possible to calculate the fraction that produced it. For example:
![]()
Multiplying each side by 10:
![]()
Subtracting the first line from the second (we can do this because it’s the same as subtracting x from both sides):
![]()
Then dividing both sides by 9, we get the fractional form of the repeating decimal.
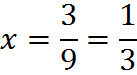
Here’s another example:
![]()
![]()
![]()
We will work with 10x and 100x so that the digits after the decimal points match and will cancel in the subtraction. Subtracting the second-to-last equation from the last-equation, we get:
![]()
Dividing by 990, we get
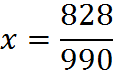
To simplify this fraction, you might see that both numerator and denominator are divisible by 9. We can use the divisibility rule, discussed earlier, that numbers whose digits sum to 9 are divisible by 9. For example, 8+2+8=18, and 18 is divisible by 9, so 828 is divisible by 9. Likewise for 990.
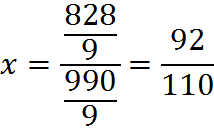
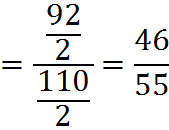
We have determined that 0.8363636… is equivalent to the fraction 46/55.
Do not be concerned if this calculation strikes you as long. Without any clue to guide you, this would be a tricky computation by GMAT standards. The key is to understand what we have done and build your familiarity in converting between fractions and decimals.
Decimals of Fractions with 9’s in the Denominator
If the repeating decimal is between 0 and 1, and the repeating block is n digits long, first occurring right after the decimal point, then the fraction (not necessarily reduced) will be the integer number represented by the n-digit block divided by the one represented by n digits 9. For example,
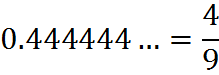

with two 9’s in the denominator since the repeating block is of 2 digits (56), and
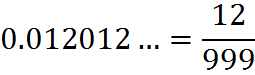
with three 9’s in the denominator since the repeating block is of 3 digits (012).
If the repeating decimal is as above, except that there are k (extra) digits 0 between the decimal point and the repeating n-digit block, then one can simply add k digits 0 after the n digits 9 of the denominator (and as before the fraction may subsequently be simplified).
For example,
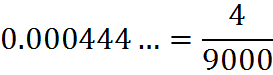
since the repeating block is 4 and this block is preceded by 3 zeroes,
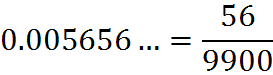
since the repeating block is 56 and it is preceded by 2 zeroes,
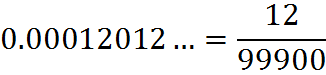
since the repeating block is 012 and it is preceded by 2 (!) zeroes.
Any repeating decimal not of the form described above can be written as a sum of a terminating decimal and a repeating decimal of one of the two above types. For example,
![]()
![]()
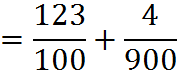
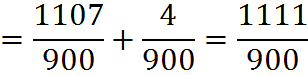
Practice Questions
Fraction of Many Decimals:
https://www.gmatfree.com/fraction-of-many-decimals
30th Digit:
https://www.gmatfree.com/30th-digit