Counting Methods, Permutations, and Combinations
Counting methods – usually referred to in GMAT materials as “combinations and permutations” – are generally the lowest-yield math area on the test. By “lowest-yield,” I mean that your score improvement on the test is low relative to the amount of effort you must put in on the topic. If you have a strong verbal showing, you can definitely break 700 or 720 without knowledge beyond counting rules #1 and #2 below. Nevertheless, if you are aiming to crush the Quantitative section and you have mastered word problems and geometry questions, it’s time to turn to counting methods.
As mentioned earlier in our discussion of factorials, on the GMAT we must sometimes count possibilities. On some questions, we do this in order to compute a probability, and on some questions, because we are asked directly to do so.
In some cases, we can count possibilities simply by enumerating them exhaustively – listing them out. That method is simple and works well on many GMAT questions. Other times, we will have to figure out the number of possibilities of something without being able to count all the possibilities, either because we are dealing with a variable or because the number of possibilities is too large to enumerate.
Rule of Product
Groups of independent possibilities, when considered conjointly, multiply in number. If there are a ways of doing one thing and b ways of doing another thing, then there are ab ways of performing both actions.
For example, suppose you decide to order pizza. You must first choose the type of crust: thin or deep dish (2 choices). Next, you choose one topping: cheese, pepperoni, or sausage (3 choices). Using the rule of product, you know that there are (2)(3) = 6 possible combinations of ordering a pizza.
Thinking of that example in notation: if the toppings are {A,B,C} and the crusts options are {X,Y}, then the possible overall selections are {AX,AY,BX,BY,CX,CY}. In this example, the rule says: multiply 3 by 2, getting 6.
The key to the rule of product is that the two categories of possibility are considered or obtained simultaneously. In other words, your pizza will have a crust type and a topping. That’s why you multiply. When you are considering mutually exclusive categories, you use the “Rule of Sum.”
Rule of Sum
The rule of sum, like the rule of product, is a basic counting principle. It is the idea that if we have a ways of doing something and b ways of doing another thing and we cannot do both at the same time, then there are a + b ways to choose one of the actions.
Consider a modification to the pizza example. Say the pizza you order, by default, is a thin-crust pizza with no toppings. At no extra cost, you can get one “enhancement” to the pizza: thick crust, or one topping – cheese, pepperoni, or sausage. The rules of the pizza store are different in this case. We can choose thick crust or a topping, but not both. Since the possibilities are exclusive, the rule of sum applies: there are 1 + 3 = 4 ways to choose the single free enhancement for your pizza.
Exercises
1. Thomas goes to a restaurant and chooses to create his own burger. He has 2 different kinds of cheese, 3 different breads, and 3 different sauces he can choose from, but he can only choose one of each category. How many different ways can he create this burger?
2. Diane is ordering pizza for her family. There are 4 different possible sizes of the pizza. Also, she has to choose one of 5 toppings to place on the pizza and one of 3 different types of cheese for the pizza. In addition, she must choose one of 3 different kinds of crust. How many different ways can she have her pizza?
3. a) How many 3-digit numbers can be formed from the digits 2, 3, 4, 5, 7 and 9?
b) How many of these numbers are less than 400?
Answers
1. 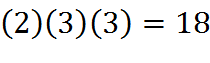
2.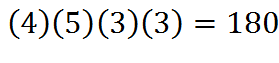
3. a) Since there are six available digits, the answer is
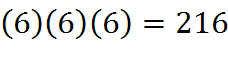
b) For the value of the 3-digit number to be less than 400, we only have two choices for the first digit, namely 2 or 3. After that we can choose the other two digits freely. The answer is thus
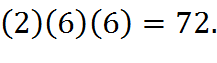
Dependent Events and Factorials
There are n! different ways of arranging n distinct objects into a sequence, the permutations of those objects.
Suppose John is working at a library. He must put 5 books on a shelf in any order. How many different ways can he order the books on the shelf? Unlike in the case of independent events, here, when John puts a book on the shelf, that eliminates one book from the remaining choices of books to put next on the shelf; thus these are referred to as dependent events. At first, he has 5 different choices, so our first number in the multiplication problem will be 5. Now that one is missing, the number is reduced to 4. Next, it’s down to 3, and so on. So, the total number of ways to order the 5 books is:
![]()
Let’s say that there are 10 dogs at a dog competition. How many different ways can one select the first-place and second-place winners? We can start with first place. There are 10 different dogs, so 10 different ways to choose the first place. Next, how many dogs are left to select the second place? In any given case, no matter who has been chosen for first place, there are 9 ways to choose second place. So, what’s the total? There are 10 ways to choose first place, and there are 9 ways to choose second place for each way to choose the first place, so there are 10 times 9 or 90 ways to choose the first place and second place out of 10 dogs. The phrase “for each,” here and often, is a clue that we should multiply.
Counting Rules
Rule 1: Repeated Trials of a Single Type. If any one of k mutually exclusive and exhaustive events can occur on each of n trials, there are
![]()
different sequences that may result from a set of such trials.
Example: Flip a coin three times, finding the number of possible sequences. Since there are two sides to a coin, there are two possible outcomes, and k = 2. There are three flips, so n = 3. Therefore,
![]()
Rule 2: Trials of Mixed Types. If the numbers
![]()
are the numbers of possibilities at n stages of events, the number of different overall sequences of events that can occur is the product of those numbers:
![]() .
.
Example: Flip a coin and roll a die, finding the number of possible sequences. The number of different overall outcomes is:
![]()
Rule 1 and Rule 2 are essentially the same rule. For example, if you consider an application of Rule 2 in which you are simply doing the same thing n times, so that all the k‘s are equal, then you end up with k to the n power possibilities. You can also mix the rules. For example, if you flip a coin three times and then roll a six-sided die, the number of possible outcomes is
![]() .
.
Rule 3: Permutation. An arrangement in order is called a permutation. The number of different ways that n distinct things may be ordered (or arranged along a line or with respect to a single dimension) is
![]()
That is, there are n! ways to order n items along a single dimension.
Example: Arrange 10 items in order, finding the number of possible ways. The number of possible arrangements is
![]()
![]()
Example: We wish to compute the number of permutations of S = {1,2,3}. Since the set S contains three elements, it has 3! = 6 permutations. They can be listed as 123, 132, 213, 231, 312, 321. This example is depicted graphically below:
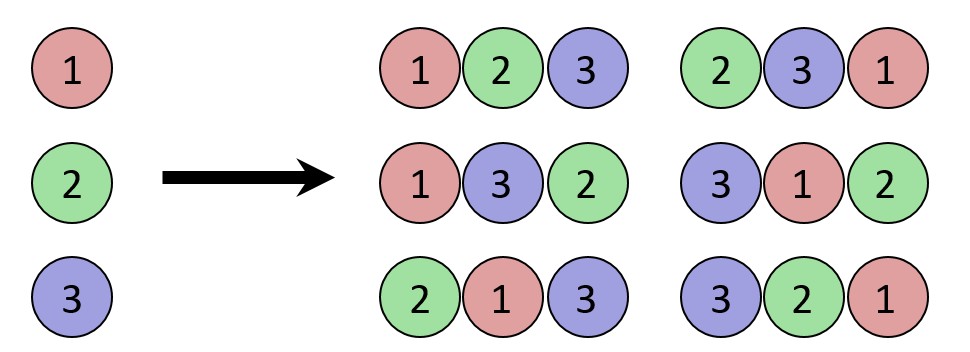
The possible permutations of 3 elements
Rule 4: k-Permutation. The number of ways of selecting and arranging k objects from among n distinct objects is:
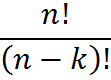
or, as seen on calculators or written by hand, [nPk].
Example: pick 3 things from 10 items, and arrange them in order. In such a case, n = 10, k = 3, so the total number of overall outcomes, selections plus arrangements, is
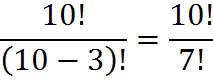
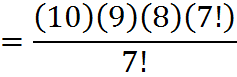
![]()
Notice how, in this calculation, the fraction of very large numbers 10!/7! was greatly simplified by reducing it to (10)(9)(8). A simplification of this nature will always be possible when applying this rule or the below rule. There will always be a factorial in the numerator and a smaller factorial in the denominator, and the factors of a larger factorial always include a smaller factorial in its entirety.
You might be able to solve this question, and other k-permutations, without using the formula above and rather using the rule of product, discussed above. Notice that the above is very similar to the example we discussed of the dog show with the two winners, only in this case, we have three winners. The same technique that we used to solve the question about the dog show could be used to solve this question.
Example: A recently formed music group has four original songs they can play. They are asked to perform two songs at a music festival. We wish to compute the number of song arrangements the group can offer in concert. Abstractly, this is equivalent to computing the number of 2-permutations of four songs. Thus, the number of distinct arrangements is 4!/2! = 12.
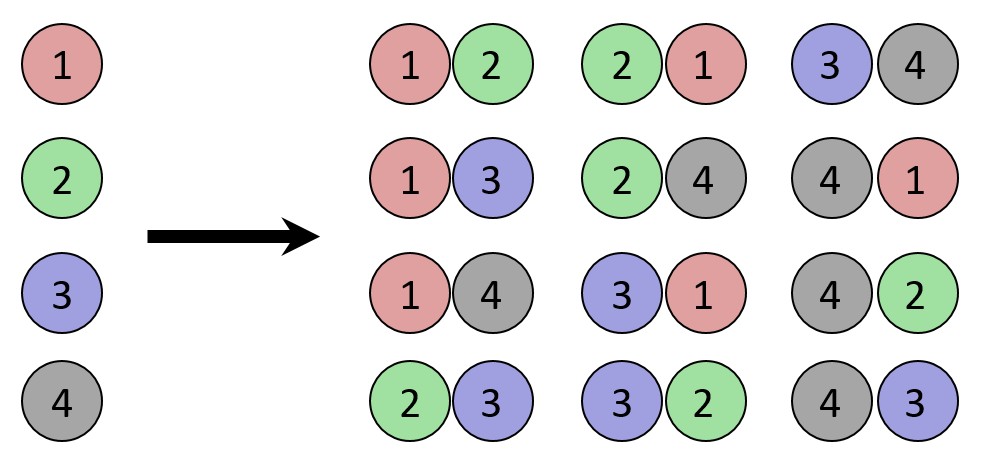
The possible choose-2 permutations of 4 items
The “choose-k” permutation of n items is similar to a simple permutation of n items, which we discussed in the previous rule. Here, there is the extra logical wrinkle that we are not choosing all of the items to go into the ordering. Another way to think about it is that the simple permutation of n items, as discussed in the prior rule, is like a choose-k permutation of n items in which you choose all n items, so that k = n. Plugging that into the formula above, we get
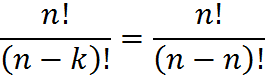
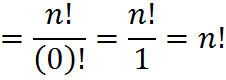
As we should expect, we have arrived back at the previous rule, which states that there are n! ways to order n items.
Rule 5: Combination. The total number of ways of selecting k distinct combinations of n objects, irrespective of order, (i.e., we are not ordering the items after we select k, but rather only doing the selection), is:
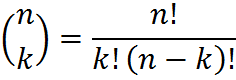
or as seen on calculators, [nCr]. This selection is called a “combination” to distinguish it from the permutation above.
Example: Pick 3 items from 10 in any order, where n = 10, k = 3. The total number of ways of making the selection is
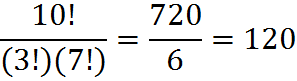
One way to remember Rule #5 is that it present a computation similar to the one in Rule 4, but in Rule 5 the quantity is made smaller by division. In this rule, Rule 5, we don’t care about order, the number of possible ways to select will be smaller, so we divide by k!.
Example: We can consider the example above in modified form. A recently formed music group has four original songs they can play. They are asked to perform two songs at a music festival. If we wish to compute the number of song arrangements the group can offer in concert, ignoring the order, the number of combinations 4!/(2!) divided by 2!, or 6.
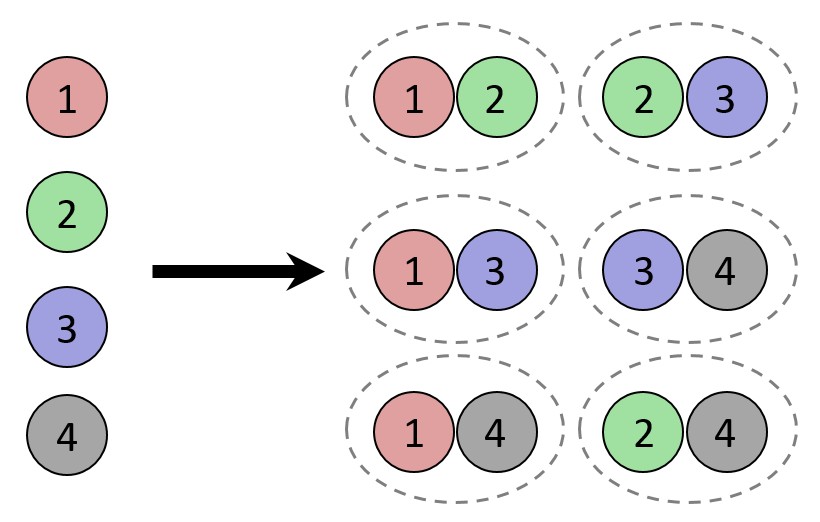
The number of combinations of 2 elements selected from 4
(The dotted lines indicate that the combinations are not ordered.)
It is sometimes useful to know that
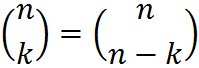
We can see this directly from the definition,
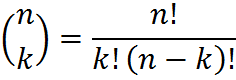
Note that the two terms in the denominator sum to n. So, for example,
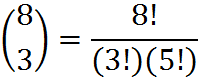
and
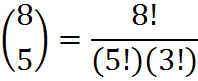
This fact could come in handy on the GMAT when you are asked for one such combination, but the equivalent combination is easier to work with.
Practice Questions
Possible Answers to a Survey:
https://www.gmatfree.com/possible-answers-to-a-survey
Assigning Pairs:
https://www.gmatfree.com/assigning-pairs