Circles

A circle is the set of all points that are at an equal distance from a center point. The distance between any of the points and the center is the radius r. The radius, in other words, is not a property of a circle – it is the defining property of a circle.

Radius, Chords, and Tangent Lines

The diameter is a line segment that connects two points on the circle and goes through the center. It is always equal in length to two radii.

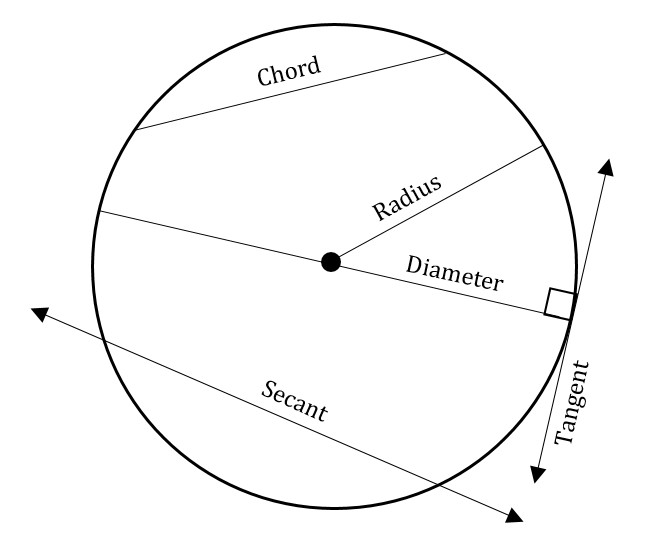
The figure above shows a circle with a diameter and a radius (of infinitely many possible diameters and radii) shown. The figure also shows a chord, a secant (which is quite similar to a chord), and a tangent line. For the GMAT, the only key facts about these other lines are:

• Any chord that is not a diameter of a circle will be shorter than the diameter of the circle.
• Any line that is tangent to a circle is perpendicular to a radius or diameter at that point, as in the figure above.

Area and Circumference

The area of a circle is given by the equation:

where r is the radius of the circle.

Here, pi is the constant number represented by the Greek letter pi equal to approximately 3.14. The number pi, like any irrational number, consists of an infinite number of non-repeating digits. (Once, for amusement, I memorized the first 1,000 digits of pi. I would wager that you could do it, too, given a month or a couple of months!) For the GMAT, you need only remember that

or, alternately put,

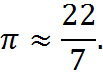
No further precision will ever be needed of you. Furthermore, answer choices will quite often be expressed in terms of pi, and in that case you will never need to express pi in digits but rather can work with it as a symbol. For example, if the radius of a circle is 4, then its area is

The circumference of a circle is its perimeter, although the term “perimeter” is generally not used with circles. The circumference of a circle is

The information required to compute area and that needed to compute circumference are identical: we need the radius and that’s all. That means that if we know a circle’s circumference, we’ll be able to compute its area, and vice versa. Also, since the diameter is simply twice the radius, knowing the diameter also will fully equip us to compute a circle’s circumference and its area. So the circumference equation, for example, is equivalent to

where d is the diameter.

That latter equation gives us a classic way to think about pi: if we rearrange it, we get

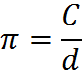
In other words, pi is the ratio of circumference to diameter of any circle. If you are bothered by pi, finding it a bit too mysterious, that fact may help to lessen the mystery (although pi is certainly mysterious and crops up in other strange places in mathematics, though these are not present on the GMAT).

Degrees, Arcs and Sections

The figure below shows a circle with radius r that has been partly shaded. The shaded region is demarcated by two radii with an angle of θ (this is the Greek letter theta) between them. In such a figure, θ is a central angle and L is an arc spanning that angle.

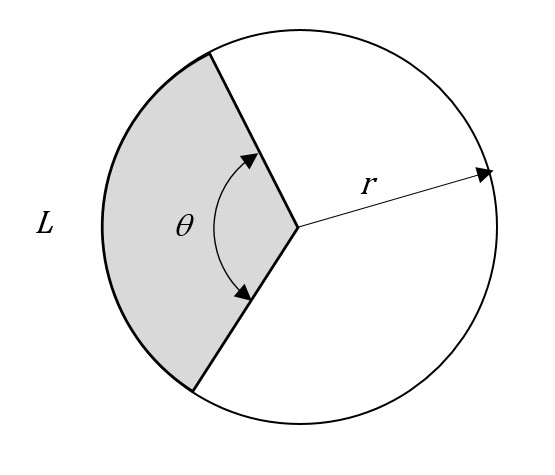Since the total span around the center point is 360 degrees, we can compare θ to 360 degrees in order to quantify the length of any arc L and the shaded area encompassed by the arc. For example, if θ were 120 degrees, then it would span one-third of 360 degrees. In that case, the length of L would be one-third of the circle’s circumference, and the area of the sector would be one-third of the circle’s area. In general,

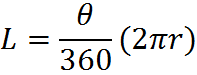
and the area of the sector is

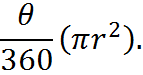
Inscribed Figures

An “inscribed” figure is one that “fits snugly” inside another shape, meaning that the shapes share points at their edges. Circles can be inscribed in other polygons, and other polygons can be inscribed in circles:

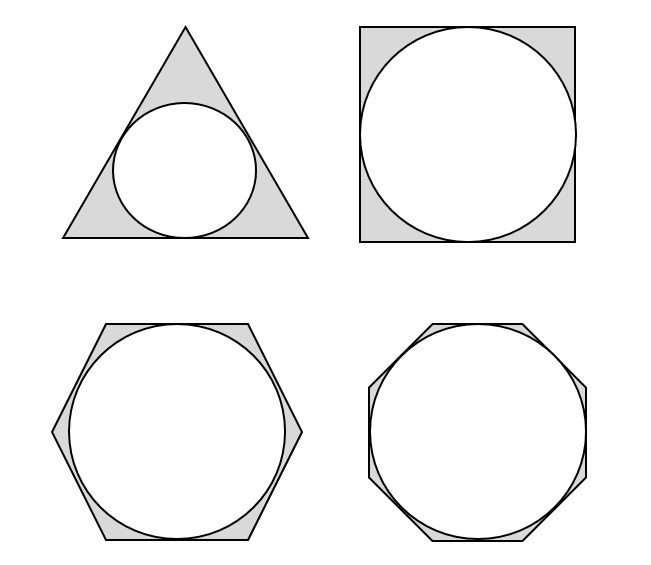
Some inscribed figures

The official GMAT languages doesn’t give you much to learn or memorize about inscribed figures. Rather, you are required simply to understand the term, so that the GMAT can give you questions in which one figure is inscribed in another and expect you fairly to understand the question.

Practically speaking, what’s usually important about inscribed figures is that you are able to infer that they share one or more dimensions. For example, consider the top-right example in the figure above, the circle inscribed in a square. If we knew that the area of the square was 9, for example, we’d be able to determine, say, the circumference of the circle. If the area of the square is 9, and we call a side of the square s, then

and hence s = 3. Since the figures are inscribed, s is equal to the diameter of the circle. Therefore, the circumference of the circle is

To be able to draw this conclusion, we have to equate s and d, and to do that use the fact that the circle is inscribed in the square.

Right Triangle Inscribed in a Circle

There is another, often overlooked, fact about inscribed figures that you must know for the GMAT. If a triangle is inscribed in a circle such that one side of the triangle is a diameter of the circle, then that triangle is a right triangle. This fact is called Thales’ theorem.

The converse is also true: if a right triangle is inscribed within a circle, then one of its sides passes through the center of the circle and is a diameter.

The theorem is summarized by the following diagram:

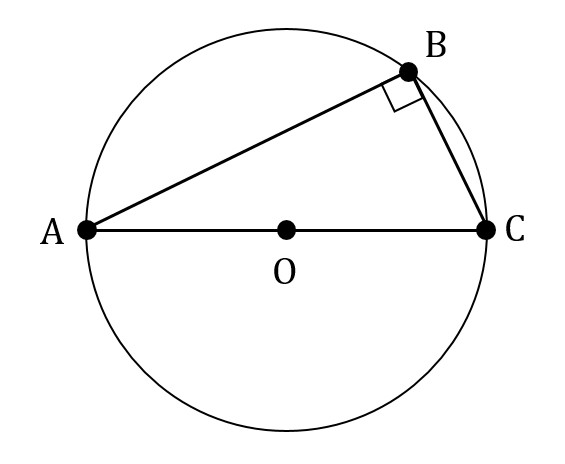
In other words, if we are given the figure above and told that O is the center of the circle and that AC passes through O, then we would be able to infer that ABC is a right triangle even without the right angle marking in the diagram.

You do not need to know why Thales’ theorem is true for the GMAT. However, you may be annoyed at not knowing why it’s true. The crux of the matter is that, in the figure above, OB is a radius of the circle. Since OA and OC are also radii of the circle, that means that AOB and COB are both isosceles triangles. From that, writing equations for the angles of these two triangles, you can prove that angle ABC = 90. Again, you don’t need to memorize the proof for the GMAT. The type of reasoning that is used in the proof, however, is typical of what you have to do on GMAT geometry questions: you find new uses and connections between different geometric facts, which, in this case, are the definition of the radius and diameter, the fact that triangles’ angles add to 180 degrees, and the fact that equal sides in triangles face equal angles.

Practice Questions

Angles and Fractions of a Circle:
https://www.gmatfree.com/angles-and-fractions-of-a-circle

Circle in the Coordinate Plane:
https://www.gmatfree.com/circle-in-the-coordinate-plane

Tangent Circle:
https://www.gmatfree.com/Tangent-Circle