Angles of Polygons
Interior and Exterior Angles of a Polygon
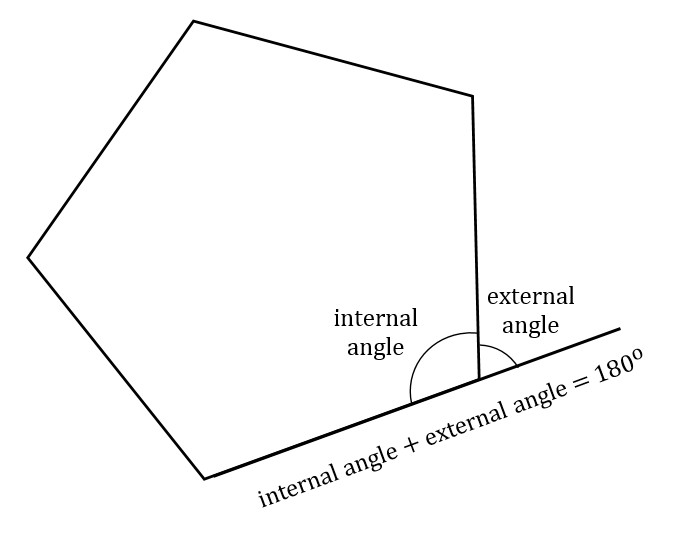
In a polygon, an interior or internal angle is one formed by two adjacent sides. An exterior or external angle is one formed by an extension of one side of the polygon, as in the figure above. As you can see in the figure, the internal angle and exterior angle of a particular vertex lie along a single line, so they must add to 180 degrees.
Sum of Interior Angles of a Polygon
The sum of interior angles of a polygon is
![]()
where n is the number of angles. For example, for a triangle, n = 3, so the sum or interior angles is
![]()
In quadrilaterals, including squares, rectangles, other parallelograms, trapezoids, and irregular quadrilaterals, the number of angles is 4, so the sum of interior angles is
![]()
How about a twelve-sided polygon? Whether it’s regular or irregular, the sum of its interior angles will be
![]()
Since the sums of angles of triangles and rectangles are easy to remember, you can use them to recall the formula 180(n – 2) degrees. All you have to remember is that for a triangle we have 180 degrees, for a quadrilateral we have 360 degrees, and that each side beyond four is that same difference, another 180 degrees.
Cutting a Polygon Into Triangles
Polygons of more than three sides can be cut into triangles by connecting the vertices with lines. As you can see in this figure, there are many ways to cut a hexagon into triangles:
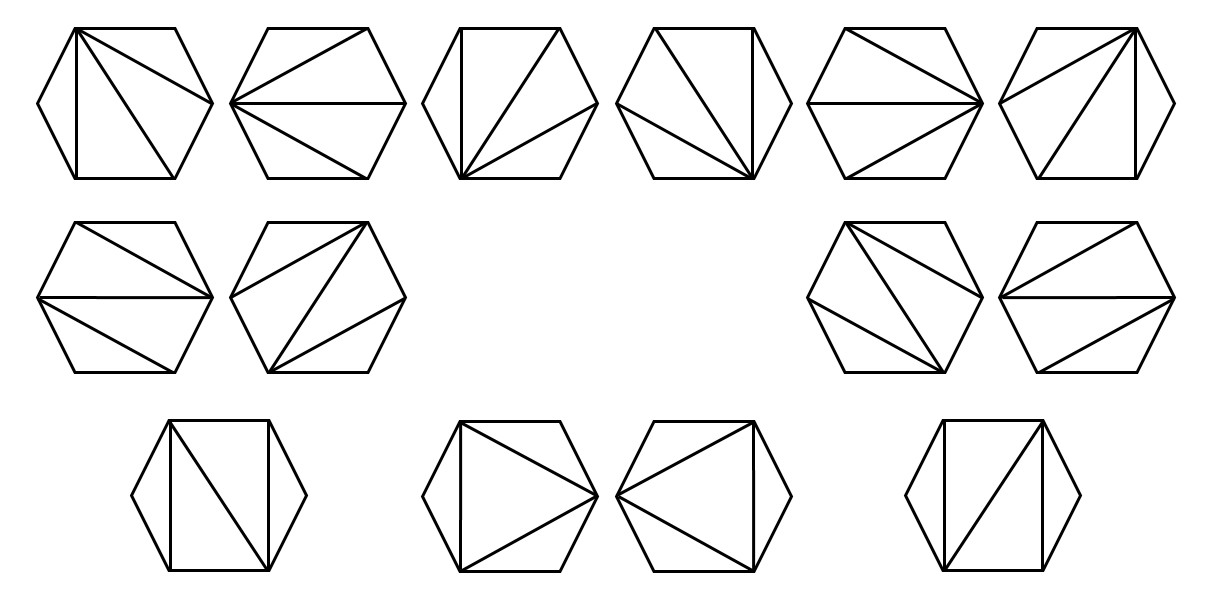
Ways to cut a hexagon into triangles
When you have to deal with any complex shape or set of shapes on a GMAT geometry question, you’ll want to attempt to view that shape in terms of component parts. After all, there are only so many concepts that are “fair game” on the GMAT, so some questions will be designed to be more difficult by putting these concepts together in unexpected ways. If you have to deal with the angles of a polygon, you have the above rule, 180(n – 2) degrees, to work with, and if you can find triangles within the figure, you can use the fact that triangle angles sum to 180 degrees and possibly one or more of the other facts about triangles covered above.
Studying the figure above, you can see that it provides an illustration of why the 180(n – 2) degrees rule is true. As you can see, the many possible ways of slicing a hexagon into triangles all contain four triangles. You may also be able to convince yourself that it’s always 4 triangles in this case because the number of vertices is 6, so that a polygon can always be cut into (n – 2) triangles. Also notice that all of the interior angles of these triangles sum up to the interior angles of the triangle, so the full 180 degrees of each triangle’s angles go into the total, which is therefore 180(n – 2) degrees. These observations can be helpful to remember and understand the 180(n – 2) degrees rule. Furthermore, when you face a difficult question with polygons and angles, keep an eye out for triangles.